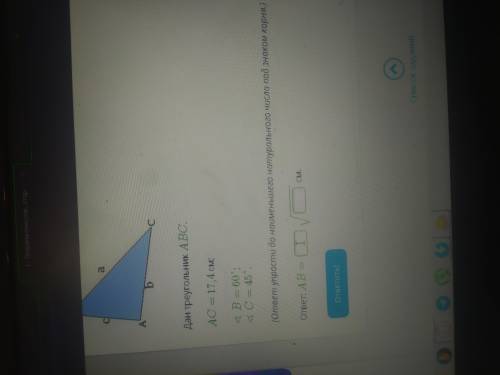
Дан треугольник ABC AC 17,4

Найти AB упростите до наименьшего натурального числа под знаком корня

Для того чтобы найти длину стороны AB треугольника ABC, нам понадобится использовать теорему Пифагора.

Теорема Пифагора гласит: в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов. В нашем случае гипотенузой является сторона AC, а катетами - AB и BC.

Используя данную теорему, мы можем записать следующее уравнение:
AB^2 + BC^2 = AC^2

Мы знаем, что AC = 17.4 см. При подстановке этого значения в уравнение, получим:
AB^2 + BC^2 = (17.4)^2

Теперь решим это уравнение. Возведем число 17.4 в квадрат:
(AB^2 + BC^2) = 302.76

Так как нам нужно найти AB, избавимся от переменной BC. Мы знаем, что BC = 9 см. Подставим это значение в уравнение и решим его:
AB^2 + (9^2) = 302.76
AB^2 + 81 = 302.76
AB^2 = 302.76 - 81
AB^2 = 221.76

Теперь найдем квадратный корень из 221.76, чтобы найти значение AB:
AB = √221.76

Прокомментируем, что значение AB будет записываться в виде корня из числа 221.76. Для упрощения значения под знаком корня до наименьшего натурального числа, нужно найти квадратный корень из 221.76 и упростить его. Найдем квадратный корень и упростим значение до наименьшего натурального числа:
AB ≈ √221.76 ≈ 14.9

Округлим значение 14.9 до ближайшего целого числа (в меньшую сторону) и получим ответ:
AB ≈ 14

Таким образом, длина стороны AB составляет примерно 14 см.