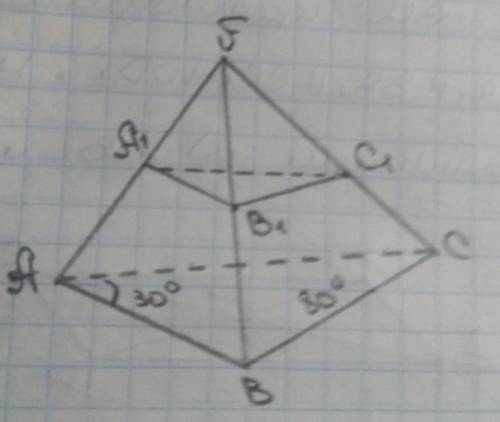
Дан треугольник ABC аа1 принадлежит bb1 принадлежит cc1 = F, A1B1 //AB, A1C1//AC, B1C1//BC, <BAC=30°,<ABC=80°. Найдите угол между прямыми
1)AB и B1C1
2) A1C1 и BC
Другие вопросы по теме Геометрия
Популярные вопросы
- Разбор слова по составу школав укр яз...
1 - 12 і 13 будь ласка вирішіть...
1 - Вычеслить дефект масс 6/3Li, если масса ядра 6,01348 а.е.м...
1 - Работа с текстом: А между тем заря разгорается; вот уже золотые полосы потянулись...
2 - 1/3×(-3×-3)-64×(-1/4×-1/4×-1/4)=...
2 - В чем появляется сходство и различие в толковании свойств достоверность и адекватность...
1 - 1. Некоторое запоминающее устройство имеет емкость 4к * 8 бит: а) сколько входов...
3 - Как деньги вернуть за подписку?...
2 - Найяскравішим представником нової європейської драми є...
2 - Т3.2. Из одной точки круговой трассы, длина которой равна 10 км, одновременно...
2
1) Найдем угол между прямыми AB и B1C1:
Из условия задачи мы знаем, что A1B1 // AB и B1C1 // BC. Также в треугольнике ABC у нас заданы углы:
Заметим, что прямые AB и AC являются сторонами треугольника ABC, а прямые B1C1 и BC - его диагоналями. Для нахождения угла между AB и B1C1 воспользуемся свойством треугольника: сумма углов треугольника равна 180°.
У нас уже известны углы
Теперь, у нас есть все углы треугольника ABC и мы можем найти угол между прямыми AB и B1C1, используя свойство параллельных прямых: если две параллельные прямые пересекают третью прямую, то сумма соответствующих углов равна 180°.
В нашем случае прямые AB и B1C1 пересекают прямую AC. Поэтому угол между AB и B1C1 равен углу ACB = 70°.
Итак, угол между прямыми AB и B1C1 равен 70°.
2) Найдем угол между прямыми A1C1 и BC:
Также, как и в предыдущем случае, мы знаем, что A1C1 // AC и B1C1 // BC. Из свойств параллельных прямых мы знаем, что если две параллельные прямые пересекают третью прямую, то сумма соответствующих углов равна 180°.
В нашем случае прямые A1C1 и BC пересекают прямую AB. Поэтому угол между A1C1 и BC равен углу BAC = 30°.
Итак, угол между прямыми A1C1 и BC равен 30°.
Надеюсь, это решение понятно школьнику. Если у него возникнут вопросы или потребуется дополнительное объяснение, пожалуйста, дайте знать.