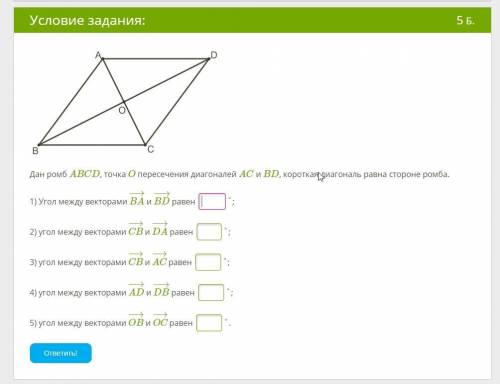
Дан ромб ABCD, точка O пересечения диагоналей AC и BD, короткая диагональ равна стороне ромба.

Для решения этой задачи, нам понадобятся некоторые свойства ромба. Давайте начнем с того, что ромб является особым видом параллелограмма, в котором все стороны равны.

Из задания нам известно, что короткая диагональ равна стороне ромба. Обозначим длину стороны ромба как x, и длину короткой диагонали как y.

Мы можем использовать свойства ромба, чтобы найти значения других сторон и диагоналей. Например, по свойству ромба, длина длинной диагонали равна удвоенной длине короткой диагонали. То есть, длина длинной диагонали равна 2y.

Также, зная, что диагонали ромба пересекаются под прямым углом в точке O, можно понять, что треугольники AOB и COD являются прямоугольными. Поскольку все стороны ромба равны, мы можем сделать вывод, что эти треугольники являются равнобедренными.

Теперь, мы можем использовать теорему Пифагора, чтобы выразить длину длинной диагонали через сторону ромба:

AO^2 + OB^2 = AB^2 (теорема Пифагора в треугольнике AOB)
DO^2 + OB^2 = DB^2 (теорема Пифагора в треугольнике DOB)

Поскольку треугольники AOB и DOB равнобедренные, то AO = OB и DO = OB. Заменяем эти значения в уравнениях:

OB^2 + OB^2 = AB^2
OB^2 + OB^2 = DB^2

Теперь, суммируем эти два уравнения:

2OB^2 = AB^2 + DB^2

Используя свойство ромба, мы знаем, что AB = x и DB = 2y:

2OB^2 = x^2 + (2y)^2
2OB^2 = x^2 + 4y^2
OB^2 = (x^2 + 4y^2)/2
OB^2 = x^2/2 + 2y^2

Теперь, мы можем выразить сторону ромба через длину длинной диагонали:

OB^2 = (x^2)/2 + 2y^2
y^2 = (OB^2 - (x^2)/2)/2
y^2 = (OB^2 - x^2/2) / 2
y^2 = OB^2/2 - x^2/4

Мы также знаем, что короткая диагональ равна стороне ромба, то есть y = x. Мы можем заменить y на x в уравнении:

x^2 = OB^2/2 - x^2/4

Теперь, выразим OB^2 через сторону ромба:

x^2 = OB^2/2 - x^2/4
4x^2 = 2OB^2 - x^2
5x^2 = 2OB^2
OB^2 = (5x^2)/2

Из этого уравнения мы видим, что OB^2 является функцией квадрата длины стороны ромба. Это означает, что если мы знаем длину стороны ромба, мы можем найти длину длинной диагонали, умножив ее на √(5/2).

Таким образом, чтобы найти длину длинной диагонали, умножим длину стороны ромба на √(5/2).

Надеюсь, что эта подробная разборка помогла вам лучше понять решение задачи и свойства ромба. Если у вас возникли еще вопросы, не стесняйтесь задавать их!