Дан ромб abcd. известно что p=72. s=156. найдите sin, cos, tg

Чтож, попробую. Найдем сначала сторону ромба. Так как периметр равен сумме 4-х одинаковых сторон, то, обозначив сторону ромба за а, получим

Р=4*а

72=4*а

а=72:4

а=18.

По известной формуле площади ромба

где а - сторона ромба,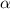 - угол между двумя его сторонами. Причем угол любой (тупой или острый - синус будет один и тот же).

Найдем синус, подставив известные площадь и сторону.

Сократим обе части на 6

Сократим на 2 обе части

Если угол острый, то косинус положительный. По основному тригонометрическому тождеству

Тангенс - это отношение синуса к косинусу, то есть при остром угле

Если угол тупой, то косинус и тангенс будут с отрицательными знаками.