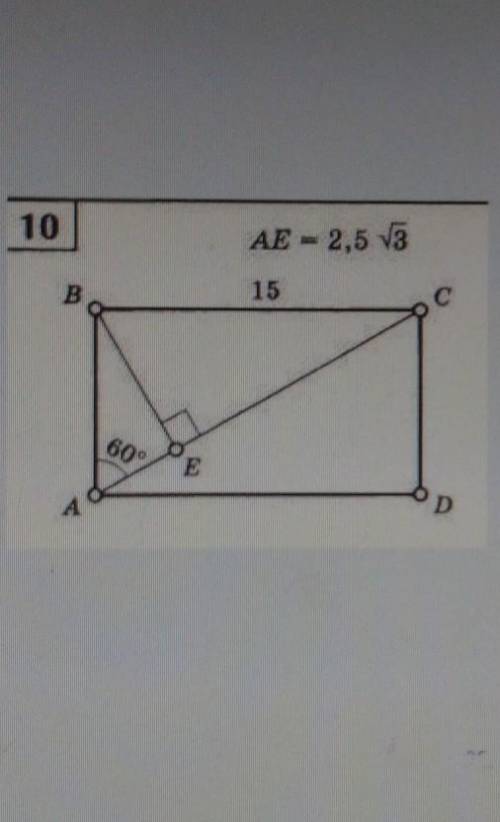
Дан прямоугольник ABCD.Диагональ ВС=15см,АЕ=2,5√3,угол А=60 градусов.Найдите площадь треугольника АВС

Для нахождения площади треугольника АВС, нам нужно знать длины двух его сторон и величину угла между этими сторонами. В данной задаче нам известны длина одной стороны (диагональ ВС) и ее угол с другой стороной (угол А). Однако, нам неизвестна длина второй стороны треугольника. Для решения этой задачи, нам понадобится использовать теорему косинусов, которая связывает длины сторон треугольника и величину углов. Теорема косинусов: В любом треугольнике, квадрат длины одной стороны равен сумме квадратов длин двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними (теорема косинусов: c^2 = a^2 + b^2 - 2*a*b*cos(C), где c - длина стороны напротив угла C, a и b - длины двух других сторон). В нашем случае, мы можем применить теорему косинусов для нахождения длины стороны АВ. Пусть АС представляет собой вторую сторону треугольника АВС. Тогда, мы можем записать: 15^2 = (2.5√3)^2 + АС^2 - 2 * (2.5√3) * АС * cos(60) Решим это уравнение для АС: 225 = 6.25 * 3 + АС^2 - 5√3 * АС 225 = 18.75 + АС^2 - 5√3 * АС АС^2 - 5√3 * АС = 225 - 18.75 АС^2 - 5√3 * АС = 206.25 Теперь, найдем значение АС.