Дан правильный шестиугольник abcdef. найдите ab, если bf = .

Рассмотрим треугольник ABF AF=AB (стороны правильного 6уг равны)

тр ABFАМ*ВМ*sinАМВ=24 равнобедренный и углы при основании равны

Рассматривая в 6 угольнике угол FAB равен 720/6=120 т.к. сумма всех углов в 6 угольнике равна 720 градусов (если провести диаметр, то получится две трапеции, а сумма углов в трапеции равна 360 градусов) и все 6 углов равны между собой.

И так в тр ABF угол при вершине 120 градусов, значит углы при основании (180-120)/2=30

проведем высоту АО к основанию BF. АО =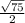 (треугольник ABF равнобедренный)

cosABO=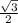=BO/AB

AB=BO/cosABO=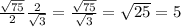

пусть АВ=х

ВF=корень из75

ВF пересекает АД в т.О.

ВО=ОF=(корень из75)/2

уголА=120градусов

треугольникАВF равнобедренный, углы при основании =(180=120):2=30

катет, лежащий против угла 30 градусов = половине гипотенузы =>

в треугольникеАВО:

х^2=(х/2)^2+((корень из 75)/2)^2

х^2=х^2/4+75/4

4х^2-х^2=75

3х^2=75

х^2=25

х=5

ответ: АВ=5см.