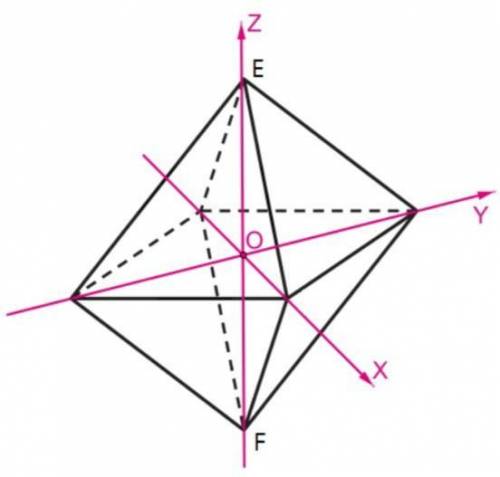
Дан октаэдр. Точка пересечения диагоналей данного октаэдра EABCDF совпадает с началом системы координат, оси которой проходят через вершины октаэдра. (На рисунке некоторые вершины не обозначены, их можно определить по имеющимся в условии координатам). Даны координаты точек D(6;0;0) и C(0;6;0).

Определи координаты точек:

A(_;_;_);

B(_;_;_);

E(_;_:_);

F(_;_;_).​

Для решения задачи по определению координат точек A, B, E и F октаэдра, нам необходимо использовать предоставленную информацию о точках D и C, а также условие о том, что точка пересечения диагоналей EABCDF совпадает с началом системы координат.

Поскольку D и C представлены в виде координат (x, y, z), мы можем предположить, что и другие точки (A, B, E, F) будут представлены тремя координатами (x, y, z).

Дано:
D(6, 0, 0) и C(0, 6, 0).

1. Определение координат точки A:
Поскольку точка A не указана на рисунке, но известно, что точка EABCDF пересекает диагонали, мы можем предположить, что координата z точки A будет отличаться от 0, поскольку точка D находится в плоскости z = 0. Тогда мы можем предположить, что координата z точки A будет равна 6, поскольку точка C также находится в плоскости z = 0.

Таким образом, координаты точки A равны (6, _, _).

2. Определение координат точки B:
Точка B также не указана на рисунке, но известно, что точка B будет находиться в той же плоскости, что и точка C (плоскость z = 0). Это означает, что координата z точки B будет равна 0.

Поскольку точка EABCDF пересекает диагонали, мы можем предположить, что точки D и B лежат на одной диагонали.

Расстояние между точками D(6,0,0) и B( x, y, 0) можно определить по формуле расстояния между двумя точками в трехмерном пространстве:
√((x2 - x1)^2 + (y2 - y1)^2 + (z2 - z1)^2) = √((x - 6)^2 + (y - 0)^2 + (0 - 0)^2)

Поскольку точки D и B лежат на одной диагонали, и точка D находится в начале системы координат, то x1 = 6, y1 = 0, z1 = 0.

Используя координаты точки C(0, 6, 0), мы получаем:

√((x - 6)^2 + (y - 0)^2 + (0 - 0)^2) = √((0 - 6)^2 + (6 - 0)^2 + (0 - 0)^2)
√((x - 6)^2 + y^2) = √(36 + 36) = √72 = 6√2

Сокращаем выражение:

(x - 6)^2 + y^2 = 72

Таким образом, у нас есть уравнение x и y, которое определяет координаты точки B.

3. Определение координат точки E:
Точка E находится в начале системы координат и совпадает с точкой пересечения диагоналей EABCDF, поэтому ее координаты будут (0, 0, 0).

4. Определение координат точки F:
Точка F также не указана на рисунке, но мы можем определить ее координаты, используя уже известные координаты других точек.

Точка F находится на противоположной диагонали от точки E. Таким образом, координата x точки F будет равна противоположной координате x точки E. Аналогично координата y точки F будет равна противоположной координате y точки E.

Поскольку точка E находится в начале системы координат, координаты точки F будут (-x, -y, -z), где x и y - координаты точки E.

Таким образом, координаты точки F будут (-x, -y, -6), где x и y - значения, которые мы найдем позднее.

Вывод:
Координаты точек октаэдра:

A(6, _, _)
B(_, _, _)
E(0, 0, 0)
F(-x, -y, -6)

Для определения остальных координат точек A, B и F требуется больше информации, например, информация о координатах точки E или других определенных точек октаэдра.