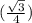Дан куб ABCDA1B1C1D1. Точка O - центр грани AA1BB1. Найдите угол между прямыми DO и CD1. Решите задачу с метода координат. (Если можно, то сделайте , с рисунком)
Другие вопросы по теме Геометрия
Популярные вопросы
- Назовите основные проблемы транспортной системы в нашей стране?...
2 - Необходимо указать метод соединение детали, там где стоят цифры....
2 - Метонимия в произведении «дубровский» олицетворение в произведении...
1 - Какую типичную психологическую ошибку допускает крупская: школа...
3 - Ссформулируйте закон действующих масс для скорости реакции....
3 - Зякою середньою швидкістю рухається місяць навколо землі, якщо...
1 - Решите уравнения 1) х+7/4 =3/1,2 2)15/21-4х =60/44 3)2/3=5-4х/7...
3 - ответьте на вопросы: 1. что такое модель? каковы основные свойства...
2 - в 1928 году итальянский генерал нобиле задумал повторить путешествие...
2 - Саргументами по на тему «когда гордость мешает быть счастливым»...
3
DO и CD₁ - скрещиваются, но А₁В ║ CD₁ ⇒ угол между прямыми DO и CD₁ равен углу между прямыми DO и А₁В. Пусть ребро исходного куба равно единице: АВ = 1, тогда диагональ грани равна корню из двух: А₁В = √2. Рассмотрим ΔDАO – прямоугольный (DА ⊥ АO), по теореме Пифагора: DO² = АO² + DА², АО = 0,5*АВ₁ =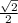 ⇒
⇒
DO² =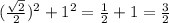 .
.
Далее рассмотрим ΔDOВ, где ∠DOВ = углу между прямыми DO и А₁В =
= углу между прямыми DO и CD₁. При этом DВ = √2 как диагональ квадрата с единичной стороной, ОВ =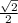 , DO² =
, DO² = 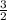 .
.
По теореме косинусов: DВ² = DO² + ОВ² – 2 · DO · ОВ · сos(∠DOВ) ⇒
√2² =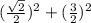
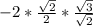 * сos(∠DOВ) ⇒
* сos(∠DOВ) ⇒
√3*сos(∠DOВ) =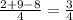 ⇒ сos(∠DOВ) =
⇒ сos(∠DOВ) = 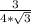 =
= 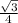 ⇒
⇒
∠DOВ = углу между прямыми DO и CD₁ = arccos