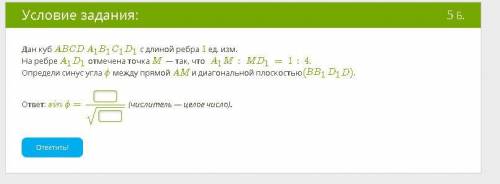
Дан куб ABCDA1B1C1D1 с длиной ребра 1 ед. изм. На ребре A1D1 отмечена точка M — так, что A1M:MD1=1:4.
Определи синус угла ϕ между прямой AM и диагональной плоскостью(BB1D1D).

Для определения синуса угла φ между прямой AM и диагональной плоскостью (BB1D1D) сначала найдем координаты точек A1, M и D1.

Так как A1M:MD1=1:4, можно предположить, что расстояние от точки A1 до точки M составляет 1/5 от всего расстояния A1D1. Поэтому, расстояние от A1 до M можно выразить как (1/5) * 1 = 1/5.

Также, расстояние от M до D1 можно выразить как (4/5) * 1 = 4/5.

Следовательно, координаты точек A1, M и D1 можно выразить следующим образом:

A1 = (0, 0, 0)
M = (1/5, 0, 0)
D1 = (4/5, 0, 0)

Для определения синуса угла φ требуется знать величину векторного произведения векторов AM и AD1, а затем разделить полученное значение на произведение модулей этих векторов.

Вектор AM можно получить, вычтя из координаты точки M координату точки A1:

AM = M - A1 = (1/5, 0, 0) - (0, 0, 0) = (1/5, 0, 0)

Вектор AD1 можно получить, вычтя из координаты точки D1 координату точки A1:

AD1 = D1 - A1 = (4/5, 0, 0) - (0, 0, 0) = (4/5, 0, 0)

Теперь вычислим векторное произведение AM и AD1.

Векторное произведение векторов AM и AD1 может быть найдено следующим образом:

AM × AD1 = [(0 * 0) - (0 * (4/5)), (0 * (4/5)) - ((1/5) * 0), ((1/5) * (4/5)) - (0 * 0)] = [0, 0, 4/25]

Значение полученного вектора [0, 0, 4/25] говорит нам о том, что векторное произведение векторов AM и AD1 равно вектору, направленному по оси Z (третьей оси координатной системы), и его модуль равен 4/25.

Теперь вычислим модули векторов AM и AD1.

Модуль вектора AM можно найти используя его координаты:

|AM| = √((1/5)^2 + 0^2 + 0^2) = √(1/25) = 1/5

Модуль вектора AD1 можно найти используя его координаты:

|AD1| = √((4/5)^2 + 0^2 + 0^2) = √(16/25) = 4/5

Теперь, синус угла φ можно вычислить, разделив модуль векторного произведения векторов AM и AD1 на произведение модулей векторов AM и AD1:

sin φ = (|AM × AD1|) / (|AM| * |AD1|) = (4/25) / ((1/5) * (4/5)) = (4/25) / (4/25) = 1

Таким образом, синус угла φ между прямой AM и диагональной плоскостью (BB1D1D) равен 1.