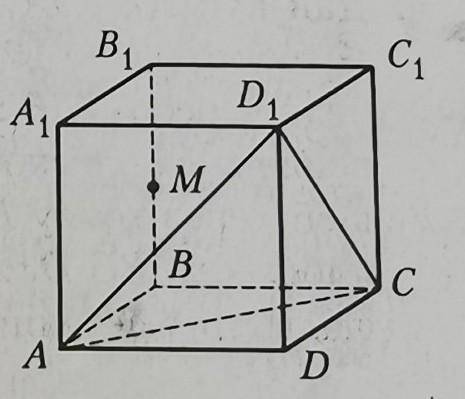
Дан Куб ABCDA1B1C1D1, ребро которого равно 12, точка M - середина ребра BB1. Постройте сечение куба плоскостью, проходящей через точку M параллельно плоскости AD1C и найдите площадь этого сечения

ты нашёл ответмы щяс нв контрольный просто

Для нахождения площади сечения куба, мы должны построить плоскость, параллельную плоскости AD1C и проходящую через точку M.

Шаг 1: Построение плоскости

Мы знаем, что M - середина ребра BB1. В кубе ABCDA1B1C1D1 ребро равно 12, поэтому BB1 также равно 12. Поскольку M находится на середине ребра BB1, то BM равно половине BB1, или BM = 12/2 = 6.

Шаг 2: Нахождение точки E

Далее нам нужно найти точку E, через которую проходит плоскость AD1C и которая лежит на линии, параллельной BB1 и проходящей через M. Так как точка M находится на середине BB1, то связанные с ней отрезки BM и BM1 также равны. Поэтому отрезок BM1, как и BM, равен 6. И так как B и B1 лежат на одной грани куба, то точки M, E и M1 также лежат на одной прямой.

Таким образом, мы можем взять точку E и построить отрезок ME, равный 6, и продолжить его на другой стороне точки E, чтобы получить отрезок EM1 такой же длины, равный 6, исходя из свойства параллельных линий. Таким образом, EM1 = 6.

Шаг 3: Построение плоскости AD1C

Поскольку плоскость AD1C проходит через точки A, D1 и C, то мы можем использовать эти точки для построения плоскости. Изобразим на плоскости точки A, D1 и C и соединим их линиями AD1, D1C и CA. Теперь мы имеем плоскость AD1C.

Шаг 4: Построение сечения

Чтобы построить сечение, нужно нарисовать плоскость, проходящую через точку M и параллельную плоскости AD1C. Мы можем использовать точки M, E и M1, чтобы построить линию, параллельную AD1C, и проложить её через точку M.

На этом этапе мы получаем сечение, которое является параллелограммом. Для нахождения площади этого параллелограмма, нам нужно найти длину его базы и высоту.

Шаг 5: Нахождение длины базы

Поскольку EM = 6, а EM1 = 6, то длина базы параллелограмма равна EM + EM1 = 6 + 6 = 12.

Шаг 6: Нахождение высоты

Высота параллелограмма определяется либо перпендикулярным отрезком, проведенным от одной из сторон параллелограмма к его противоположной стороне, либо с помощью формулы, использующей площадь параллелограмма. Так как нам известна площадь сечения, мы можем использовать соотношение между высотой и площадью:

Площадь сечения = длина базы * высота

Нам необходимо найти высоту. Подставив данную площадь и длину базы, мы можем решить уравнение:

Площадь сечения = 12 * высота

Таким образом, высота будет равна Площадь сечения / 12.

Шаг 7: Нахождение площади сечения

Подставляя значение длины базы и высоты в формулу площади параллелограмма, мы получаем:

Площадь сечения = 12 * высота

Теперь мы можем подставить значение высоты, которую мы нашли в предыдущем шаге, и решить эту формулу для нахождения площади сечения.

Это пошаговое решение поможет школьнику понять, как построить сечение куба и найти его площадь.