Дан куб ABCDA1B1C1D1. На рёбрах B1C1 и C1D1 соответственно отмечены точки N и M так, что B1N:NC1=1:1;C1M:MD1=1:3.
Определи косинус угла α между прямыми BN и CM, если ребро куба равняется 1 ед. изм.
ответ: cos α=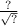
Другие вопросы по теме Геометрия
Популярные вопросы
- Прочитайте в хрестоматии 14-ю главу. Сопоставьте образы Петра Анг евича...
2 - 10. Назвіть термін за його визначенням: «Елементи, що не впливають на розвиток...
2 - Твір публіцистичного стилю із порівняльним зворотом про культуру 15-20...
3 - 7 Спишите. Укажите, чем выражена именная часть сказуемого. Определите раз-...
3 - Написати лист для работорговців...
2 - Выберите источники географической информации. Аэрокосмические снимки Транспорт...
3 - Что такое клетка (у человека)...
2 - Обществознание шестой класс свой пример ограниченным возможностям...
3 - Краткое содержание истории России 7 класс Н.М.Арсеньев 9 параграф...
1 - Составить вапросы на тему Ночь перед Рождеством...
2
1. Построим координатную систему с началом в точке A и осями, параллельными ребрам куба.
2. Обозначим координаты точек: A(0, 0, 0), B(1, 0, 0), C(1, 1, 0), D(0, 1, 0), A1(0, 0, 1), B1(1, 0, 1), C1(1, 1, 1), D1(0, 1, 1), N(x, 0, 1), M(1, y, 1), где x и y - координаты точек N и M соответственно.
3. Найдем вектора BN и CM.
- Вектор BN = B - N = (1 - x, 0, 0 - 1) = (1 - x, 0, -1)
- Вектор CM = C - M = (1 - 1, 1 - y, 0 - 1) = (0, 1 - y, -1)
4. Найдем скалярное произведение векторов BN и CM.
BN * CM = (1 - x)*(0) + (0)*(1 - y) + (-1)*(-1) = 1 + x - y
5. Найдем модули векторов BN и CM.
|BN| = √[(1 - x)^2 + (0)^2 + (-1)^2] = √[1 + x^2 - 2x + 1] = √(x^2 - 2x + 2)
|CM| = √[(0)^2 + (1 - y)^2 + (-1)^2] = √[1 + y^2 - 2y + 1] = √(y^2 - 2y + 2)
6. Найдем значение косинуса угла α между прямыми BN и CM, используя формулу для косинуса угла между векторами:
cos α = (BN * CM) / (|BN| * |CM|)
Подставим значения:
cos α = (1 + x - y) / (√(x^2 - 2x + 2) * √(y^2 - 2y + 2))
Таким образом, косинус угла α между прямыми BN и CM равен (1 + x - y) / (√(x^2 - 2x + 2) * √(y^2 - 2y + 2)).