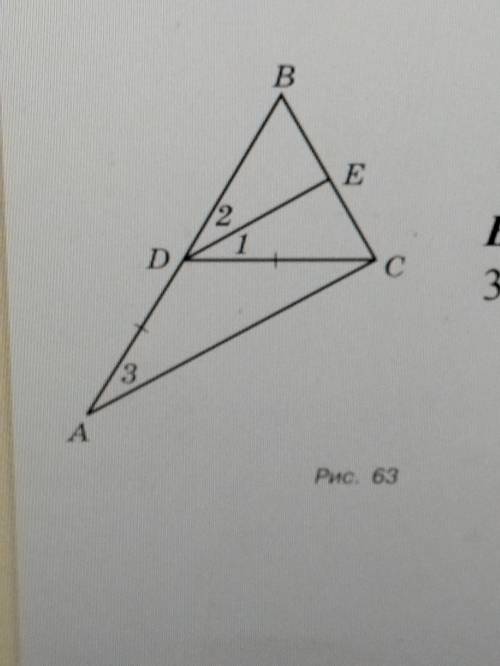
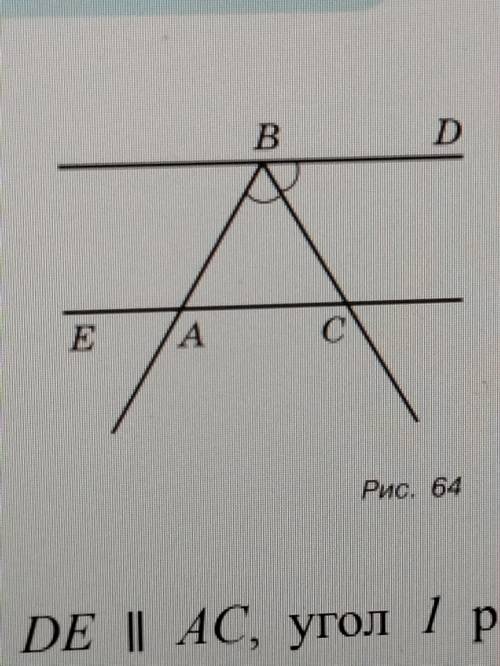
Д) На рисунке 64 BD || АC, луч BC - биссектриса угла ABD, L EAB = 116°. Найдите угол BCA. E) На рисунке 63 AD = DC, DE I| AC, угол равен 30°. Определите градусные меры углов 2 и 3.

Добрый день! Давайте разберемся с задачами по геометрии.

D) На рисунке 64 BD || АC, луч BC - биссектриса угла ABD, L EAB = 116°. Найдите угол BCA.

Для начала, давайте проведем несколько небольших шагов для более ясного понимания.

1. Заметим, что угол EAB является внутренним углом треугольника ABC. Поэтому, сумма углов BAC и BCA должна быть равна 180°.
BAC + BCA = 180° ............(1)

2. Также известно, что луч BC является биссектрисой угла ABD. Это означает, что угол DBA равен углу DBC.
DBA = DBC ............(2)

3. Зная, что BD || AC, мы можем применить теорему о параллельных линиях. В неравенстве треугольников ABD и BDC можно сказать, что
углы ABD и BDC, оба внутренние углы треугольников, должны быть равными.
ABD = BDC ............(3)

Теперь давайте воспользуемся полученными уравнениями для нахождения угла BCA.

Из уравнения (3) мы знаем, что углы ABD и BDC равны. Так как угол DBA равен углу DBC (из уравнения 2), то мы также можем сказать, что угол DBA равен углу ABD (по транзитивности равенства углов).
DBA = ABD ............(4)

Теперь мы можем использовать уравнения (1) и (4) для нахождения угла BCA.
BAC + BCA = 180° ............(1)
DBA + BCA = 180° (подставляем уравнение 4)
ABD + BCA = 180° (так как DBA и ABD равны)

Поскольку мы знаем, что угол EAB равен 116° (по условию), мы можем подставить это значение и решить уравнение.
116° + BCA = 180°

Теперь найдем угол BCA:
BCA = 180° - 116° = 64°

Ответ: угол BCA равен 64°.

E) На рисунке 63 AD = DC, DE || AC, угол равен 30°. Определите градусные меры углов 2 и 3.

1. Заметим, что угол 2 и угол 3 являются внутренними углами треугольника ABC. Поэтому, сумма углов 1, 2 и 3 должна быть равна 180°.
1 + 2 + 3 = 180° ............(5)

2. Так как DE || AC, то по теореме о параллельных линиях углы 3 и угол 2 являются соответственными (они находятся на параллельных линиях и пересекаются одним и тем же углом).
3 = 2 ............(6)

3. Известно, что угол 1 равен 30° (по условию).
1 = 30° ............(7)

Теперь давайте воспользуемся полученными уравнениями для нахождения углов 2 и 3.

Из уравнений (5), (6) и (7) мы можем выразить углы 2 и 3 в терминах угла 1.
1 + 2 + 3 = 180° ............(5)
30° + 2 + 2 = 180° (подставляем уравнение 7)
2 + 3 = 180° - 30° = 150°
2 + 2 = 150° (по уравнению 6)
4 = 150°
2 = 150° - 4 = 146°

Ответ: угол 2 равен 146°.

Также использовав уравнение (5), мы можем найти угол 3:
30° + 2 + 3 = 180°
33 + 3 = 180°
3 = 180° - 33 = 147°

Ответ: угол 3 равен 147°.

Надеюсь, эти пошаговые решения помогут вам понять задачи и получить правильный ответ!

Если у вас возникнут еще вопросы, не стесняйтесь задавать их. Я всегда готов помочь.