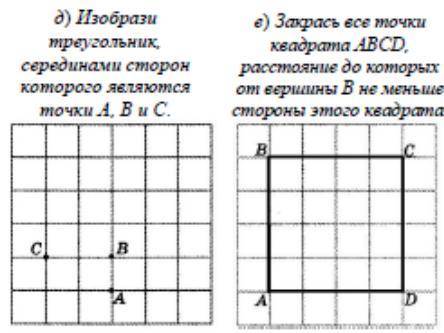
Д) Изобразите треугольник, серединами сторон которого являются точки А, В и С. Е) Закрасьте все точки квадрата ABCD, расстояние до которых от вершины В не меньше стороны этого квадрата.

Для решения этой задачи, давайте начнем с построения треугольника, серединами сторон которого являются точки А, В и С.

1. Задачу мы можем решить, используя свойство медиан треугольника. Медиана - это отрезок, соединяющий вершину треугольника с серединой противоположной стороны.

2. Для начала, построим отрезки, которые будут являться медианами треугольника. Медиана из вершины А будет соединять вершину А с серединой стороны ВС. Медиана из вершины В будет соединять вершину В с серединой стороны АС. Медиана из вершины С будет соединять вершину С с серединой стороны AB.

3. Чтобы найти середину стороны треугольника, нужно соединить две точки, являющиеся концами этой стороны и провести серединный перпендикуляр. Найдем середину стороны ВС. Для этого проведем прямую, перпендикулярную стороне ВС, через точку В. Аналогично найдем середины сторон AC и AB. Обозначим их точками D, E и F соответственно.

4. Теперь соединим полученные точки А, B и С линиями. Мы получили треугольник ABC, серединами сторон которого являются точки D, E и F.

Теперь перейдем к заданию Е, которое требует закрасить все точки квадрата ABCD, расстояние до которых от вершины В не меньше стороны этого квадрата.

1. Найдем расстояние от вершины В до одной из сторон квадрата ABCD. Заметим, что сторона квадрата AB совпадает с отрезком ВD. Следовательно, сторона квадрата ABCD равна длине отрезка ВD.

2. Чтобы найти все точки квадрата ABCD, расстояние до которых от вершины В не меньше стороны этого квадрата, нужно закрасить все точки внутри квадрата, а также все точки на его границе.

3. Теперь, найдем точки, которые лежат на границе этого квадрата ABCD. Границы квадрата ABCD образуют стороны этого квадрата и отрезки, соединяющие середины соседних сторон.

4. Закрасим точки внутри квадрата ABCD, а также точки на его границе, используя найденные отрезки и линии.

На рисунке видно, что закрашены точки внутри квадрата ABCD, а также точки на его границе, расстояние от которых до вершины В не меньше стороны этого квадрата.

Таким образом, мы успешно нашли треугольник, серединами сторон которого являются точки А, В и С, и закрасили все точки квадрата ABCD, удовлетворяющие условию задания Е.