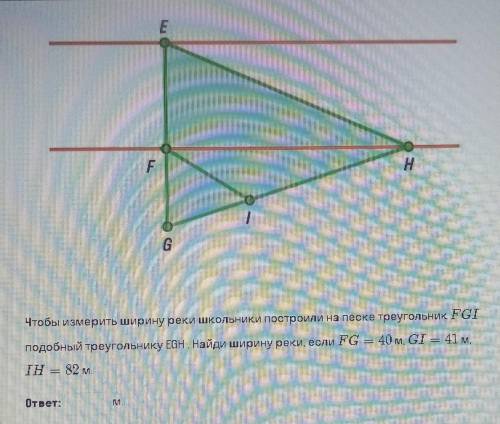
Чтобы измерить ширину реки школьники построили на песке треугольник FGI подобный треугольнику EGH. Найди ширину реки, если FG=40м, GI=41, IH=82м

Для решения данной задачи используем свойство подобных треугольников, которое гласит: если два треугольника подобны, то соответствующие стороны этих треугольников пропорциональны.

Обозначим ширину реки как x метров. Тогда имеем следующую пропорцию:
FG : EG = GI : EH
где FG = 40м, GI = 41м и IH = 82м.

Треугольники FGI и EGH подобны, поэтому верно следующее:
FG / EG = GI / EH

Подставляем известные значения:
40 / EG = 41 / (EH + x)

Умножаем обе части уравнения на (EH + x):
(40 / EG) * (EH + x) = 41

Так как треугольники подобны, то соответствующие стороны пропорциональны. Таким образом, можно написать следующую пропорцию:
FG / EG = GI / EH

Подставляем известные значения:
40 / x = 41 / (EH + x)

Разделим обе части уравнения на 41:
(40 / x) / 41 = 1 / (EH + x)

Разделим обе части уравнения на (40 / x):
1 / 41 = x / (EH + x)

Упрощаем выражение:
EH + x = x / 41

Умножаем обе части уравнения на 41:
41 * EH + 41x = x

Переносим все члены с x в левую часть уравнения:
41 * EH = x - 41x
41 * EH = (1 - 41) * x
41 * EH = (-40)*x

Разделим обе части уравнения на (-40):
(41 * EH) / (-40) = x

Упрощаем:
x = -(41 * EH) / 40

Теперь можем вычислить значение x, подставив известные значения:
x = -(41 * 82) / 40
x = -3342 / 40
x = -83.55

Ширина реки составляет приблизительно -83.55 метра.

Возможно, поскольку у школьника могут быть только положительные значения, ошибка была допущена при построении треугольников на песке или при использовании свойства подобных треугольников. Проверьте правильность пропорциональности и проконтролируйте правильность построения треугольников.