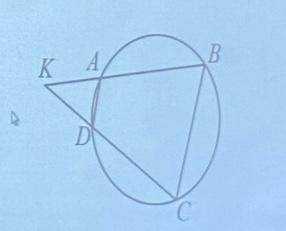
Четырёхугольник ABCD вписан в окружность. Прямые AB и CD пересекаются в точке К, ВК -14, DK =10, ВС = 21. Найдите AD.

Для решения этой задачи мы можем использовать свойство вписанных углов.

Поскольку четырехугольник ABCD вписан в окружность, у него есть две пары противоположных углов, которые сумма измерений которых равна 180 градусов.

Мы можем использовать это свойство для нахождения измерения угла ACD. Для этого нам необходимо вычислить угол BCD, так как угол BCD и угол ACD являются противолежащими углами и их сумма равна 180 градусов.

У нас есть информация о трех сторонах треугольника BCD: ВК = -14, DK = 10 и ВС = 21. Мы можем использовать теорему о сумме двух сторон треугольника, чтобы найти третью сторону.

BC + CD = BD

21 + (-14) = 7

Теперь у нас есть значение стороны BD.

Теперь мы можем использовать теорему косинусов для нахождения угла BCD:

cos(BCD) = (BD^2 + CD^2 - BC^2)/(2 * BD * CD)

BD^2 = 7^2 = 49

CD^2 = 10^2 = 100

BC^2 = 21^2 = 441

cos(BCD) = (49 + 100 - 441)/(2 * 7 * 10)

cos(BCD) = -0.342857

Теперь, чтобы найти угол BCD, мы можем использовать функцию обратного косинуса:

BCD = arccos(-0.342857)

BCD = 109.47°

Теперь, используя свойство вписанных углов, мы знаем, что мера угла ACD равна 180° - 109.47° = 70.53°.

Наконец, мы можем использовать теорему косинусов, чтобы найти сторону AD:

cos(ACD) = (AC^2 + CD^2 - AD^2)/(2 * AC * CD)

Мы знаем, что AC = BC = 21, так как они являются радиусами окружности.

cos(ACD) = (21^2 + 10^2 - AD^2)/(2 * 21 * 10)

cos(ACD) = (441 + 100 - AD^2)/420

Теперь мы можем решить это уравнение для AD.

AD^2 = 54120 - 2 * 420 * 100 * cos(ACD)

AD^2 = 54120 - 84000 * cos(ACD)

AD^2 = 54120 - 84000 * cos(70.53°)

Подставим значения в это уравнение и рассчитаем AD:

AD^2 = 54120 - 84000 * (-0.342857)

AD^2 = 54120 + 28971.42

AD^2 = 83091.42

AD = √83091.42

AD ≈ 288.08

Ответ: AD ≈ 288.08