1. Геометрия
  2. Четырёхугольник ABCD

Четырёхугольник ABCD трапеция угол А=64 градуса Найдите угол между векторами BА и AD ответы не нужны, решение!!

ser73 ser73    3   25.10.2021 11:34    7

Ответы
AlyaMrr AlyaMrr  01.12.2021 03:57

\boxed{ \angle(\overrightarrow{BA}, \overrightarrow{AD}) = 116^{\circ} }

Объяснение:

Дано: ABCD - трапеция, ∠A = 64°,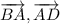 \overrightarrow{BA}, \overrightarrow{AD}

Найти: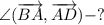 \angle(\overrightarrow{BA}, \overrightarrow{AD}) - ?

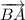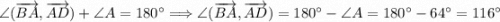Решение: Для того, чтобы найти угол между перенесем векторы в одну точку, так чтобы начала векторов имели общую точку. Сделаем параллельный перенос вектора \overrightarrow{BA} так, чтобы точка B перешла в точку A .Угол \angle(\overrightarrow{BA}, \overrightarrow{AD}) смежный с угол ∠A. По свойству смежных углов их сумма 180°, следовательно:\angle(\overrightarrow{BA}, \overrightarrow{AD}) + \angle A = 180^{\circ} \Longrightarrow \angle(\overrightarrow{BA}, \overrightarrow{AD}) = 180^{\circ} - \angle A = 180^{\circ} - 64^{\circ} = 116^{\circ}.


Четырёхугольник ABCD трапеция угол А=64 градуса Найдите угол между векторами BА и AD ответы не нужны
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
9763 9763  12.09.2019 11:17
Расставьте буквенные обозначения проекции...
evelinastepenko evelinastepenko  12.09.2019 11:18
1.. 7. в каком случае прямые а и b параллельны (рис. 2): . . а) 21 = 88°, 26 = 92° б) 22: = 103°, 23 = 779 в) 23=75°, 25 = 105° г) 28 = 110°, 24 = 110° д) 27 = 81°, 23 = 89°...
Ученицав Ученицав  12.09.2019 11:19
впиши в окошки нужное слово (в окошке могут быть также два слова). в параллелограмме углы . выбери правильный вариант ответа. в дано ( свойство признак параллелограмма....
keklol1990 keklol1990  12.09.2019 11:25
Нижнее, . только полное решение...
bayrzhan bayrzhan  03.06.2019 01:50
Диагональ ас прямоугольника abcd равна 3 см и составляет со стороной ad угол в 42°. найдите площадь прямоугольника abcd...
оля2029 оля2029  03.06.2019 01:50
Найдите нули функции y=x^3-x^2+x-1; y=8x^4-125x; y=2x^5+54x^2...
katyasaveleva2001 katyasaveleva2001  03.06.2019 01:50
Высота bd прямоугольного треугольника abc равна 24 см. и отсекает от гипотенузы ас отрезок dc равен 18 см. найдите аb и cos a...
Katyusha4368 Katyusha4368  03.06.2019 01:50
Прямые aa1 и bb1 перпендикулярны к ребру ab двугранного угла, принадлежащие равным граням угла. докажите, что если aa1 перпендикулярно bb1, то данный двугранный угол - прямой...
юрий201 юрий201  03.06.2019 01:50
Дан прямоугольник abcd ,в котором диагональ ac 3 см,а угол а вместе со стороной аd равен 37 градусов .найдите площадь...
alianna366 alianna366  03.06.2019 01:50
Хорда ав и ас стягивают дуги в 60 и 120 градусов.радиус окружности равен r.найдите площадь заштрихованной фигуры. решить...

Популярные вопросы