Через вершину прямого угла прямоугольного треугольника с катетами 6 и 8 см проведен перпендикуляр к гипотенузе. вычислите площади образовавшихся треугольников.
Другие вопросы по теме Геометрия
Популярные вопросы
- Мальчик сбежал вниз по движущемуся эскалатору и насчитал 30 ступенек....
1 - Какое давление воздуха называют нормальным?...
3 - В.в.чаплина как зоотехник перехитрил оленей 1.тема: 2.идея: !...
3 - Учимся сочинять. ты любишь мечтать о том, что будет в будущем?...
1 - Сообщение роль воробьинообразных, голенастых в природе...
1 - Зубная система млекопитающих отличается от других позвоночных...
1 - Стоимость реализованной продукции составила 2500 тыс. руб., а...
2 - Какая точка принадлежит графику функции у = 3х-9? а) (0; 3) б)...
1 - Разобрать по составу слово подъезжать....
3 - Расплескалось в шумном беге. определить падеж в слове (беге)...
1
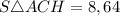 см²;
см²; 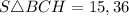 см².
см².
Объяснение:Обозначим данный треугольник буквами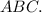
======================================================
Проведём высоту к гипотенузе
к гипотенузе 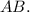
======================================================
По теореме Пифагора найдём гипотенузу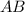 :
:
Пусть -
- 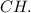
======================================================
По теореме Пифагора найдём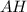 :
:
S( ΔAHC) = 15,36см² ; S(ΔCHB)= 8,64 см².
Объяснение: