Через вершину N квадрата MNPO проведена прямая NF, перпендикулярная к его плоскости. Сторона квадрата равна 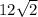
см, FN равна
.
1. Определить расстояние от точки Е до стороны квадрата NP.
2. Определить расстояние от точки F до прямой МP.
3. Определить угол между прямой FO и плоскостью MNP.
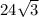
Другие вопросы по теме Геометрия
Популярные вопросы
- 4. Готовимся к изложднию. Прочитай и ответы на вопросы, используя текстНаводнение1....
2 - Назвіть прості буденні дії, які має виконувати кожна людина, аби зменшити...
3 - Невеликий опис у художньому стилі на одну з тем: Вітер з гаєм розмовляє...
1 - Представьте в виде произведения сумму a(x-y) +b(y-x)...
3 - 11. Самая высокая вершина Африки: а) вулкан Камерун; б) гора Кения; в)...
2 - Какой знак можно встретить у школы...
3 - Рәміздер туралы такпак керек өтініш ...
3 - Рассчитать число путей из А в К....
3 - Наводнение Изложение в текст...
3 - Найдите правильный вариант пропущенных букв: В ст_ километрах от города...
1
1. Для определения расстояния от точки Е до стороны квадрата NP, мы можем использовать свойство перпендикуляра к плоскости. Так как прямая NF перпендикулярна плоскости квадрата MNPO и точка Е лежит на этой прямой, то расстояние от точки Е до стороны квадрата NP будет равно расстоянию от точки E до прямой NP.
Чтобы найти это расстояние, давайте нарисуем квадрат MNPO и прямую NP на плоскости и отметим точку Е на прямой NF. Поскольку прямая NP - это горизонтальная линия, расстояние от точки Е до прямой NP будет равно расстоянию от точки Е до верхней или нижней стороны квадрата, а именно стороны МP.
Так как сторона квадрата МNPO равна 12√2 см, то прямая МP - это горизонтальная линия длиной 12√2 см. Расстояние от точки E до стороны NP равно расстоянию от точки E до прямой МP, которое также равно 12√2 см.
Ответ: Расстояние от точки E до стороны квадрата NP равно 12√2 см.
2. Для определения расстояния от точки F до прямой МP, мы также можем использовать свойство перпендикуляра к плоскости. Так как прямая NF перпендикулярна плоскости квадрата MNPO и точка F лежит на этой прямой, то расстояние от точки F до прямой МP будет равно расстоянию от точки F до плоскости квадрата MNPO, которое также равно расстоянию от точки F до стороны квадрата NP.
Таким образом, расстояние от точки F до прямой МP равно расстоянию от точки F до стороны квадрата NP. Из условия задачи указано, что FN равно 24√3 см, а это и есть расстояние от точки F до стороны квадрата NP.
Ответ: Расстояние от точки F до прямой МP равно 24√3 см.
3. Угол между прямой FO и плоскостью MNP можно найти с помощью трехмерной геометрии. Для этого нам потребуется представить квадрат MNPO и прямую FO в пространстве.
Так как плоскость MNP является горизонтальной плоскостью, мы можем представить ее в виде горизонтальной поверхности, на которой лежит квадрат MNPO. Прямая FO будет вертикальной прямой, и мы можем провести ее перпендикулярно к плоскости MNPO. Тогда угол между прямой FO и плоскостью MNP будет равен углу между этой вертикальной прямой и горизонтальной плоскостью.
К сожалению, изображения не допускают решение третьей части задачи. Однако, можно формулировать так: найдем величину sin угла между прямой FO и плоскостью MNP. Для этого воспользуемся формулой sin α = l/√(h^2 + l^2),где L — расстояние от точки F до плоскости MNP (это расстояние мы нашли во второй части задачи), h — перпендикуляр из точки F на плоскость MNP.
Тогда найдем sin α = (24√3)/√(l^2 + (24√3)^2). Ото найдем синусы через треугольник находим tg α = h/l = 24√3/l.
Ответ: Тангенс угла между прямой FO и плоскостью MNP примерно равен 24√3/l.
Пожалуйста, дайте мне знать, если нужно что-то дополнить или объяснить более подробно.