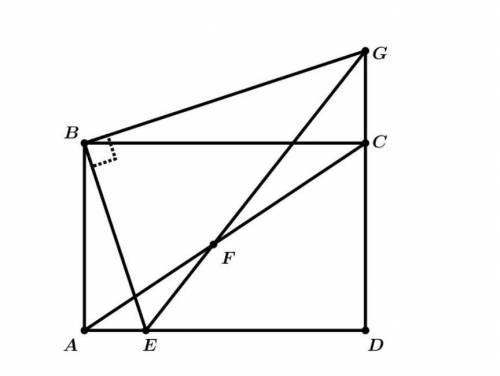
Через вершину B прямоугольника ABCD провели две перпендикулярные прямые. Первая прямая пересекла сторону AD в точке E, а вторая — продолжение стороны DC за точку C в точке G. Отрезки EG и AC пересекаются в точке F. Выберите 4 точки: точку и 3 точки, лежащие на прямой Симсона этой точки относительно некоторого треугольника, вершины которого изображены на картинке. Все 7 точек должны быть различны.
Другие вопросы по теме Геометрия
Популярные вопросы
- Написати твір-нарис про Ольгу Кобилянську...
2 - На рисунке 1 показаны фигуры симметричные относительно точки О....
2 - Укажите уравнения, для которых число 0,5 является корнем. а) 5...
3 - написати 3 речення : У кожної людини є своя співуча пір їнка....
1 - Прочитати с.167 І все таки до тебе думка лине і складіть 3 запитання...
3 - Put the verbs into the correct tense form (Past Simple, Past Perfect...
3 - это надо знать до суботты буду благодарен...
3 - Какое число надо вписать в окошко, чтобы равенство60= 8+77стало...
2 - Какое из утверждений неверно?...
3 - Что НЕЛЬЗЯ делать при укусе гадюки?...
2
Точки A-F-C лежат на прямой Симсона точки B относительно треугольника EGD.
Объяснение:
Основания перпендикуляров, опущенных из произвольной точки описанной окружности на стороны треугольника (или их продолжения), лежат на прямой Симсона.
Точка B лежит на описанной окружности треугольника EGD (прямые углы EBG и EDG опираются на диаметр EG).
A и С - основания перпендикуляров из точки B на стороны треугольника EGD.
Тогда AC - прямая Симсона точки B относительно треугольника EGD.
(Прямая Симсона пересекает сторону EG в точке F, следовательно BF⊥EG)