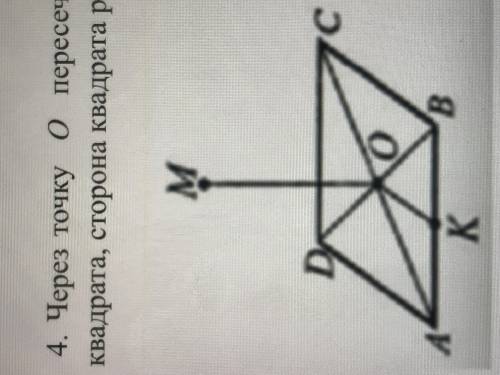
Через точку o пересечения диагоналей квадрата ABCD проведён перпендикуляр MO к плоскости квадрата сторона квадрата равна 2a. Найдите расстояние между прямыми AB и MO
Другие вопросы по теме Геометрия
Популярные вопросы
- Придумайте про винипуха с десятичными дробями....
3 - Какой частью речи является слово до плохая шутка до добра не доведёт....
1 - На какой высоте должен лететь самолет чтобы его тени не было на земле...
2 - Как решить эти примеры(c-4)(d-3), (x+y)(x+1), (a+b)(a+b), (a+2b)(2a+b)...
3 - Озеро абрау какая вода пресная , солоноватая или солёная ?...
1 - Complete the exchanges. 1.a: to the cinema on tuesday evenning? b: i m i...
2 - Периметр прямокутника 46 см . діагональ дорівнює 17 см . знайти сторони...
1 - Всаду 3 яблони и 5 груш чего больше и на сколка....
3 - Расчитать концентрацию гидроксид-ионов в растворе ph которого равен 6?...
1 - Яка тема ідея твору шевченка марія и план?...
2
1. Возьмем две точки A и B, принадлежащие стороне AD и BC соответственно, и построим их перпендикуляры к стороне CD. Обозначим эти перпендикуляры как AE и BF.
- Так как квадрат ABCD является прямоугольником, то AE и BF равны стороне CD. Отсюда, пусть AE = BF = CD = 2a.
2. Рассмотрим точку P, которая является серединой стороны CD (точка пересечения AE и BF). Расстояние от точки P до прямоугольника ABCD равно полусумме диагоналей прямоугольника. Отсюда, расстояние от точки P до точки B равно a.
3. Отметим точку O, являющуюся пересечением диагоналей квадрата ABCD. Расстояние от точки O до прямой AB равно расстоянию от точки O до точки P. Пусть это расстояние равно d.
4. Так как MO перпендикулярен плоскости квадрата ABCD, то он также перпендикулярен к прямой AB. Поэтому, расстояние между прямыми AB и MO равно d.
В итоге, ответ на вопрос задачи "Найдите расстояние между прямыми AB и MO" равен d.
Таким образом, чтобы найти расстояние от точки O до прямой AB, нужно найти расстояние от точки O до точки P.
Для этого рассмотрим треугольник OBP. Треугольник OBP является прямоугольным, так как основание BP параллельно стороне CD прямоугольника ABCD, и MO перпендикулярен AB.
Так как точка P является серединой стороны CD, то BP равняется a. Также, мы знаем, что расстояние от точки O до точки P равно d.
Для нахождения расстояния PB, можно воспользоваться теоремой Пифагора, которая утверждает, что в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.
Таким образом, имеем:
OP^2 = OB^2 - BP^2
Подставляя известные значения, получаем:
d^2 = (2a)^2 - a^2
d^2 = 4a^2 - a^2
d^2 = 3a^2
d = √(3a^2)
Таким образом, расстояние между прямыми AB и MO равно √(3a^2).