Через середину радиуса шара проведена плоскость перпендикулярная радиусу. какую часть радиуса шара составляет радиус круга получившегося сечения?
Ответы
Радиус круга в сечении - это один катет прямоугольного треугольника, половина радиуса шара - это другой катет. Гипотенузой будет радиус шара. Можно найти Cos угла между радиусом (гипотенузой) и половиной радиуса (катетом) как их отношение. Получаем что Cos = 1/2. Найти второй катет (радиус окружности в сечении) можно найти через Sin этого угла, который можно найти зная что,  . Получаем
. Получаем 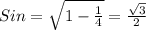 . Ну и тогда получаем, что радиус окружности в основании составляет
. Ну и тогда получаем, что радиус окружности в основании составляет  радиуса шара
радиуса шара
ПОКАЗАТЬ ОТВЕТЫ
 . Получаем
. Получаем 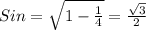 . Ну и тогда получаем, что радиус окружности в основании составляет
. Ну и тогда получаем, что радиус окружности в основании составляет  радиуса шара
радиуса шара
Другие вопросы по теме Геометрия
Популярные вопросы
- Модерн - направление в искусстве рубежа XIX-ХХ веков, претворенным образом...
1 - Среди направлений русской живописи начала XX века наиболее близко поэтике...
2 - В произведении «Последний кабак у заставы», _ достигает большой выразительной...
3 - Декоративное панно «Сеча при Керженце» Н.К. Рериха свидетельствует о влиянии...
3 - Особняк Г.А. Тарасова на Спиридоновке в Москве архитектора И. Жолтовского...
2 - Верны ли утверждения? А) Историческая заслуга Антокольского в том, что...
3 - В искусстве рубежа XIX - XX веков за обновление художественного языка,...
2 - Расположите картины в хронологическом порядке «Искушение» Шильдера «Прерванное...
3 - Статую Петра _делал для памятника, и, подобно своим предшественникам –...
1 - В.А. Серов вышел из состава действительных членов Академии Художеств в...
2