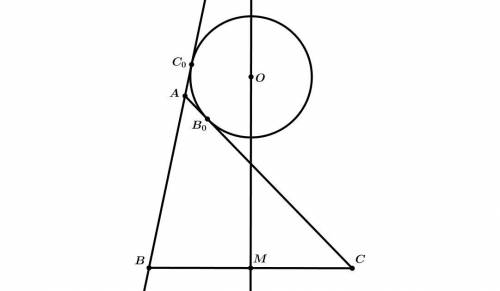
Через середину M стороны BC треугольника ABC проведён серединный перпендикуляр к стороне BC. Окружность с центром на этом серединном перпендикуляре касается стороны AC в точке B0, а продолжения стороны AB за точку A — в точке C0. Выберите на картинке 4 точки: точку и 3 точки, лежащие на прямой Симсона этой точки относительно некоторого треугольника, вершины которого изображены на картинке.
A
B
C
B0
C0
M
O

Добрый день! Давайте разберем вместе эту задачу.

В задаче дан треугольник ABC и через середину M стороны BC проведен серединный перпендикуляр к стороне BC. Задача состоит в том, чтобы найти 4 точки на прямой Симсона относительно некоторого треугольника, вершины которого изображены на картинке.

Прежде чем найти эти точки, давайте разберемся, что такое прямая Симсона. Прямая Симсона это прямая, проходящая через точку M перпендикулярно отрезку BC. Она получает свое название в честь английского математика и физика Томаса Симсона. Прямая Симсона имеет несколько интересных свойств, одно из которых нам поможет решить данную задачу.

Теперь, чтобы найти 4 точки на прямой Симсона относительно данного треугольника, нам понадобится уточнить, к какому изображенным на картинке треугольников относятся эти точки.

Обратите внимание на точки B0 и C0. Они являются точками касания окружности, проходящей через точки B0 и C0 с прямой AC. Заметим, что если мы проведем отрезок B0C0, то получим медиану треугольника ABC, так как точка M - середина стороны BC.

Теперь вернемся к прямой Симсона. Конечные точки этой прямой - это точки пересечения прямых, проходящих через точки B0 и C0 и перпендикулярных сторонам треугольника ABC. Обозначим эти точки D и E.

Таким образом, ответом на задачу будет точка D, точка E, точка B0 и точка C0.

Давайте повторим пошаговое решение:
1. Проведите медиану треугольника ABC, проходящую через точку M и точки касания окружности с прямой AC B0 и C0.
2. Найдите точки пересечения этой медианы с перпендикулярными сторонам треугольника.
3. Обозначьте эти точки как D и E.
4. Обозначьте точки B0 и C0.
5. Получите ответ: точка D, точка E, точка B0 и точка C0.

Надеюсь, это поможет вам понять и решить данную задачу. Если у вас есть еще вопросы, не стесняйтесь задавать их!"