Чему равна гипотенуза в равнобедренном прямоугольном треугольнике с катетом 10 дм

ответ: 14

Объяснение:

По теореме Сосницкого сумма квадратов сторон равна квадрату гипотенузы, поэтому ответ 10*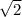 = 14

Хорошо, давайте разберем этот вопрос подробно.

Первым шагом, нужно понять, что такое равнобедренный прямоугольный треугольник. Это треугольник, у которого два катета (стороны, прилегающие к прямому углу) равны между собой.

Таким образом, в данном случае, у нас есть треугольник, у которого один катет равен 10 дм (дециметров).

Для решения задачи, мы можем использовать теорему Пифагора, которая гласит: в прямоугольном треугольнике с катетами a и b, гипотенуза (самая длинная сторона, противоположная прямому углу) равна квадратному корню из суммы квадратов катетов.

Таким образом, применяя теорему Пифагора, мы можем вычислить длину гипотенузы для данного треугольника.

По формуле теоремы Пифагора: c² = a² + b²
где c - гипотенуза, a и b - катеты.

В данном случае, катет a равен 10 дм, катет b равен также 10 дм.

Подставим значения в формулу:
c² = 10² + 10²
c² = 100 + 100
c² = 200

Для того чтобы найти значение гипотенузы (c), мы должны вычислить квадратный корень из 200:

c = √200

Теперь мы можем упростить это значение. Найдем, если возможно, квадратный корень из 200.

Мы можем разложить 200 на простые множители: 200 = 2 * 2 * 2 * 5 * 5.

Теперь мы можем использовать свойство квадратных корней: √(a * b) = √a * √b.

Подставляя значения, получим:
√200 = √(2 * 2 * 2 * 5 * 5) = √(2 * 2) * √(2 * 5 * 5) = 2 * 5 * √2 = 10√2.

Таким образом, гипотенуза равна 10√2 дм.

Вот и весь ответ. Если у тебя остались какие-либо вопросы или что-то нужно дополнительно объяснить, обязательно говори.