Большей стороны треугольника mnk является...
С решением
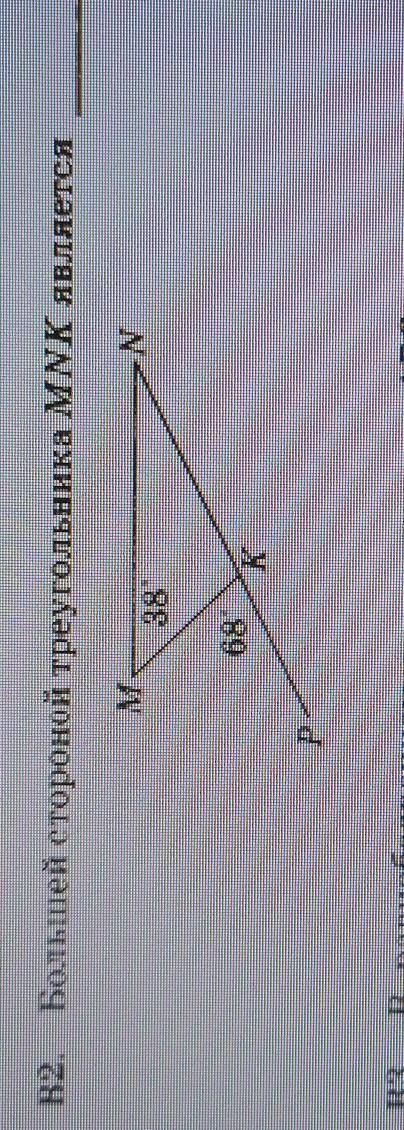
Другие вопросы по теме Геометрия
Популярные вопросы
- Сообщение на тему значение процессов жизнедеятельности у живых организмов...
2 - Что такое смешанные числа и как их решать ?...
3 - Написать другу письмо-обращение,не слишком сложное,не слишком большое. 6 класс...
3 - Определи обьем и массу 5 моль хлора...
2 - При нормальных условиях газу сообщено количество теплоты и объем газа увеличился...
3 - Групповая характеристика чиновников. из произведения ревизор ....
2 - До яких речовин - простих чи складних - належить сірка? ...
2 - Спишите определённо-личные предложе-ния. поставьте глагол-сказуемое в нужной форме.1....
2 - Спортсмен парашютист выполняет затяжной прыжок .какова масса парашютиста в полёте...
2 - укажите направление этой силы ...
3
ответ: MN
Объяснение:
Так как визуально эта сторона длиннее остальных двух
На изображении даны отрезки MK, KJ и JN, и нам нужно определить, какая из них является большей стороной треугольника MNK.
Для начала, нам необходимо определить длины данных отрезков. Для этого можно использовать масштаб на оси x и y, а также информацию о точках, которые обозначены буквами на графике.
1. Определение длины отрезка MK:
- На оси x можно определить, что расстояние между точками M и K составляет 8 единиц.
- На оси y можно определить, что расстояние между точками M и K составляет 4 единицы.
Используя теорему Пифагора (a^2 + b^2 = c^2) для прямоугольного треугольника с катетами a = 8 и b = 4, мы можем определить длину гипотенузы (c), которая будет равна:
c^2 = 8^2 + 4^2
c^2 = 64 + 16
c^2 = 80
c = √80
c ≈ 8,94
Таким образом, длина отрезка MK ≈ 8,94.
2. Определение длины отрезка KJ:
- На оси x можно определить, что расстояние между точками K и J составляет 3 единицы.
- На оси y можно определить, что расстояние между точками K и J составляет 8 единиц.
Используя теорему Пифагора для прямоугольного треугольника с катетами a = 3 и b = 8, мы можем определить длину гипотенузы (c), которая будет равна:
c^2 = 3^2 + 8^2
c^2 = 9 + 64
c^2 = 73
c = √73
c ≈ 8,54
Таким образом, длина отрезка KJ ≈ 8,54.
3. Определение длины отрезка JN:
- На оси x можно определить, что расстояние между точками J и N составляет 5 единиц.
- На оси y можно определить, что расстояние между точками J и N составляет 4 единицы.
Используя теорему Пифагора для прямоугольного треугольника с катетами a = 5 и b = 4, мы можем определить длину гипотенузы (c), которая будет равна:
c^2 = 5^2 + 4^2
c^2 = 25 + 16
c^2 = 41
c = √41
c ≈ 6,40
Таким образом, длина отрезка JN ≈ 6,40.
Теперь мы можем сравнить длины сторон треугольника MNK:
Длина MK ≈ 8,94
Длина KJ ≈ 8,54
Длина JN ≈ 6,40
Из полученных значений видно, что большей стороной треугольника MNK является отрезок MK, так как его длина наибольшая и составляет примерно 8,94 единиц.