Боковая поверхность правильной восьмиугольной пирамиды (рис. 11) равна 25, а высота 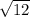. Найдите радиус вписанной в ее основание окружности.

Для решения этой задачи мы можем использовать связь между боковой поверхностью пирамиды и радиусом вписанной окружности основания.

Известно, что боковая поверхность равна 25, а высота пирамиды (h) равна √12. Мы можем найти высоту боковой грани (hb) пирамиды, используя теорему Пифагора:

hb² = h² - r², где hb - высота боковой грани, h - высота пирамиды, r - радиус вписанной окружности основания.

Зная значение высоты пирамиды и значение высоты боковой грани, мы можем найти значение радиуса, используя формулу:

r = √(h² - hb²).

В данной задаче нам не известно значение hb, поэтому нам нужно его вычислить. Однако, у нас есть основание восьмиугольная пирамида, что означает, что у нас есть правильный восьмиугольник, в котором все стороны равны.

Давайте рассмотрим правильный восьмиугольник. У него есть восемь равных радиусов, которые являются сторонами основания пирамиды. Обозначим радиус основания пирамиды как R.

Можно разбить правильный восьмиугольник на восемь треугольников, каждый из которых имеет сторону R и высоту hb. Таким образом, площадь поверхности правильного восьмиугольника можно выразить как сумму площадей восьми треугольников:

25 = 8 * (1/2 * R * hb).

Мы знаем, что каждый треугольник имеет площадь (1/2 * сторона * высота), а также что их всего восемь.

Теперь мы можем выразить высоту боковой грани hb через радиус основания R:

25 = 4R * hb.

Из этого уравнения можно найти hb:

hb = 25 / (4R).

Теперь, используя найденное значение hb и значение h, мы можем найти радиус вписанной в основание пирамиды окружности:

r = √(h² - hb²) = √(√12² - (25 / (4R))²).

Таким образом, мы можем найти радиус вписанной окружности, подставив известные значения в данную формулу.