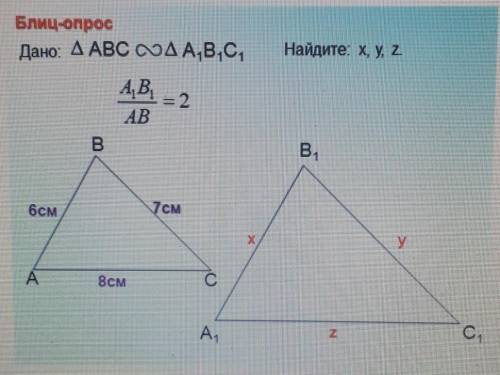
Блиц-опрос
Дано: АВС ~А1,В1,С1,
Найдите. x, y, z.
Другие вопросы по теме Геометрия
Популярные вопросы
- Новый год в произведениях Писателей Укажи тип текста. Посмотреть текст рассуждение...
3 - Как вы думаете, изменился бы порядок городов в списке, если бы список составляли...
2 - На скільки градусів можна нагріти воду масою 22 кг, спаливши гас масою 100г. якщо...
1 - y = exp(x) - (sin(x)\(sqrt(fabs(x - 7; Нужно решить уравнение с языка программирование...
3 - 2. Рассмотри таблицу. ответь на вопросы...
1 - . Гаухар задумала число. это задуманное число она разделила на (-0,6),затем от полученного...
2 - Який з наведених нижче рухів є періодичним? A Качання човна на хвилях. Б Хід маятника...
2 - Выберите верные утверждения. Крупные лесопромышленные комплексы созданы в Братске...
3 - 10. Виберіть правильні твердження щодо розвитку газовидобувної промисловості світу...
2 - Эти два номера номер 4 и 5 и 6 ч объяснением и решениемтема Квадратная функция...
3
12см 14см 16см
Объяснение:
A1B1/6=2
A1B1=6×2
A1B1=12(см)
аналогично
B1C1=7×2=14(см)
C1A1=8×2=16(см)
Чтобы решить эту задачу, мы должны использовать свойство подобных треугольников - соотношение сторон.
Поскольку треугольники АВС и А1В1С1 подобны, отношение длины любой стороны АВС к соответствующей стороне А1В1С1 будет одинаковым.
Таким образом, мы можем записать соотношение между сторонами:
AB / A1B1 = BC / B1C1 = AC / A1C1
Мы можем использовать данное свойство для решения задачи. Найдем соотношение между сторонами AB и A1B1.
AB / A1B1 = AC / A1C1
Из заданного нам вопроса видно, что отношение заменяет каждую сторону треугольника А1В1С1 на соответствующую сторону треугольника АВС.
Значит, мы можем написать:
10 / x = 25 / 20
Для нахождения x, мы можем использовать пропорцию. У нас есть отношение AB / A1B1 = 10 / x, и мы знаем, что это отношение равно 25 / 20.
Мы можем установить пропорцию:
AB / A1B1 = 10 / x = 25 / 20
Для решения этой пропорции, мы можем умножить крест-накрест:
AB * 20 = A1B1 * 10
200 = A1B1 * 10
A1B1 = 200 / 10
A1B1 = 20
Таким образом, x = 20.
Поскольку треугольник АВС подобен треугольнику А1В1С1, мы можем использовать ту же самую пропорцию для нахождения y:
BC / B1C1 = AB / A1B1 = 10 / y
Мы знаем, что AB = 10 и A1B1 = 20, поэтому:
BC / B1C1 = 10 / y = 10 / 20
BC * 20 = B1C1 * 10
200 = B1C1 * 10
B1C1 = 200 / 10
B1C1 = 20
Таким образом, y = 20.
Теперь, чтобы найти z, мы можем использовать последнее отношение:
AC / A1C1 = AB / A1B1 = 10 / z
Мы знаем, что AB = 10 и A1B1 = 20, поэтому:
AC / A1C1 = 10 / z = 10 / 20
AC * 20 = A1C1 * 10
200 = A1C1 * 10
A1C1 = 200 / 10
A1C1 = 20
Таким образом, z = 20.
Итак, значения x, y и z равны 20 каждое.