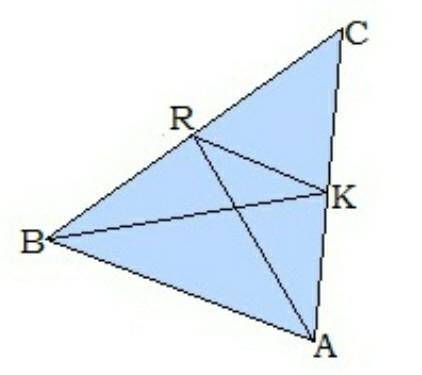
Bk и ar медианы
BR=10
AK=11
RK=5
найти P(ABC)​

Для решения данной задачи, нам понадобится использовать свойства медиан треугольника и понятия площади треугольника.

Дано, что Bk и ar являются медианами треугольника ABC. Мы также знаем, что BR = 10, AK = 11 и RK = 5.

По свойству медианы треугольника, медиана делит линию, на которой она лежит, на две равные части. То есть, BK = KC и AR = RC.

Давайте обозначим точку пересечения медиан BK и AR как точку M. Также обозначим точку пересечения AM и BK как точку N.

Теперь у нас есть многоугольник BMNK, в котором все стороны равны между собой (BM = MN = NK), так как они являются медианами и точкой пересечения медиан является точка М, то BMNK - параллелограмм (поскольку противоположные стороны параллельны и равны).

Чтобы найти площадь треугольника ABC можно использовать площадь параллелограмма BMNK. Площадь параллелограмма можно найти умножив длину любой из его сторон (например, BM) на высоту, опущенную на эту сторону (например, высота, опущенная на сторону BN).

Найдем сторону BM:
BM = BK + KM
Так как BMKN - параллелограмм, то BM = NK = 5

Теперь найдем высоту BN:
Обратимся к треугольнику BMK. Он является прямоугольным, так как MN является медианой и делит сторону BK пополам.
Используя теорему Пифагора, мы можем найти сторону BN:
BN^2 = BM^2 - MN^2
BN^2 = 5^2 - 2.5^2
BN^2 = 25 - 6.25
BN^2 = 18.75
BN = √18.75

Теперь у нас есть все необходимые данные, чтобы найти площадь треугольника ABC:
P(ABC) = 0.5 * BM * BN
P(ABC) = 0.5 * 5 * √18.75

После подстановки численных значений в формулу и решения математических операций, вы получите ответ.