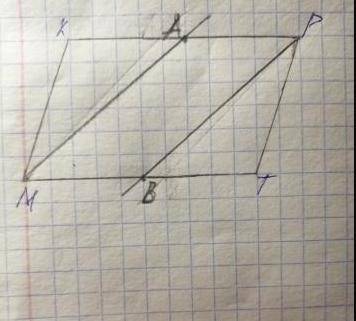
Биссектрисы углов M и P параллелограмма MKPT пересекают стороны KP и MT соответственно в точках A и B.
а) Докажите, что отрезки MA и PB равны.
б) Вычислите периметр парралелограмма MKPT, если KA = PA, AB = 12см.
Другие вопросы по теме Геометрия
Популярные вопросы
- Нарисуйте графики функций , найдите точки x и y , где прямая пересекает оси...
2 - Массовая доля азота в нитриде кальция (Ca3N2) равна...
1 - В библиотеке 45 книг разделили на стопки по одинаковому количеству книг в каждой...
1 - You have been asked to write a story for a magazine for young people. Your...
3 - Он алты жасар чемпион тақырыбы мен идеясы...
1 - Чому перші писані закони Русі виникли у часи Ярослава Мудрого...
2 - составить план и понять идею текста...
2 - За до додаткових джерел охарактеризуйте становище основних верств населення...
1 - Построить таблицу истинности для логического выражения: ¬(x ∧ y) ∨ z...
2 - Кто сможет ?швоашатадаьщаьадаьащаьат...
3
72
Объяснение:
а) треугольники MKA и BPT равны по двум углам и стороне (MK=PT, углы K равны T, и углы KMA и BPT равны (биссектрисы равных углов.) (параллелограмм)). Значит, MA = PB (против равных углов - равные стороны).
б) проведем AB, получим два равных параллелограмма (KABM и ABPT), где AB равно КM и PT, а значит бок. стороны равны по 12, а стороны KA и AP равны, то есть сторона KP равна 24, тогда периметр 48 + 24 = 72