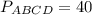Биссектрисы углов а и д параллелограмма авсд пересекают сторону вс в точках к и м соответственно, причем вк=км=мс, ак=8, дм=6. найдите периметр паралелограмма
Другие вопросы по теме Геометрия
Популярные вопросы
- Обчисліть який обєм повітря (н.у) необхідний для спалювання метану обємом 60...
1 - ДО ТЬ БУДЬ ЛАСКА Потрібно написати кілька речень даю Уявіть, що ви на Гаїті...
3 - Кипятильник нагревает 1.2 кг воды от температуры 20 градусов по Цельсия до кипения...
2 - Present Perfect or Present Perfect Continuous - 1 Fill in with the correct form...
1 - Вставь пропущенные буквы в однокоренные слова :гл( )зной,п( )виц, м( )мной,...
3 - Причины возникновения творческого импульса....
2 - Визнач закономірність і допиши два наступних числа. 102; 253; 404... На скільки...
2 - 6.Обмеження сфер, де використовується національна мова, що приводить до знекровлення...
3 - Природні зони якого поясу найбільш поширені в Північній Америц Скажіть будь-ласка....
3 - SOS! SOS! SOS! SOS! SOS! Яких відтінків лексичного значення набувае слово ляльковий»...
3
Чертеж к решению - во вложении.
Известно, что биссектрисы двух непротивоположных углов параллелограмма пересекаются под прямым углом и отсекают равнобедренные треугольники. Таким, образом, треугольники АВК и МСД равнобедренные, а треугольник КРМ - прямоугольный.
Все равные углы (накрест лежащие и вертикальные), а также равные отрезки отмечены на чертеже.
Ведем обозначения: ВК=КМ=МС=х, КР=у, МР=z.
Периметр параллелограмма P=2(АВ+ВС)=8х.
Треугольники РАД и РКМ подобны по двум углам. Поэтому
1)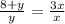
3y=8+y
y=4,
2)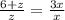
z+6=3z
z=3,
По теореме Пифагора в треугольнике КРМ
ответ: