1. Геометрия
  2. Биссектрисы треугольника ABCпересекаются

Биссектрисы треугольника ABCпересекаются в точке P .Найдите длину отрезка CP,если AB=AC=5,BC=8

mashkakornilova mashkakornilova    2   07.08.2021 18:25    6

Ответы
sashanepasha sashanepasha  06.09.2021 18:57

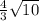
ответ: \frac{4}{3} \sqrt{10}

Объяснение:

пусть AP пересекает BC в точке M, тогда M - середина BC и CM=BC/2=4. По теореме Пифагора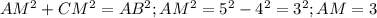 AM^2+CM^2=AB^2; AM^2=5^2-4^2=3^2; AM=3. Верен следующий факт: бисектрисса делит сторону на отрезки, пропорциональные прилежащим сторонам. Отсюда \frac{AP}{AC}=\frac{PM}{CM}; \frac{AP}{PM}=\frac{AC}{CM}=\frac{5}{4} ; \frac{PM}{AM} =\frac{4}{9}; PM=\frac{4}{3}. По теореме Пифагора CP^2=PM^2+CM^2=(\frac{4}{3})^2+4^2=10(\frac{4}{3})^2; CP=\frac{4}{3}\sqrt{10}

P.s. Это восьмой класс

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Геометрия
Amalia1337 Amalia1337  10.12.2020 13:43
Як називають теорему яка безпосередньо впливає з аксіоми чи іншої теореми?...
aruka10511 aruka10511  10.12.2020 13:44
Дано куб ABCDA1B1C1D1 пряма BC перпендикулярна площині.​...
stoyanovadsДарья stoyanovadsДарья  10.12.2020 13:44
В прямоугольном треугольнике a и b - катеты, c - гипотенуза.Найдите a, если b=2√35 и c=12...
НиколайСПБ НиколайСПБ  10.12.2020 13:45
Із точки A до площини α проведено перпендикуляр AO, довжина якого дорівнює 1 см, і дві рівні похилі AB і AC, що утворюють із перпендикуляром кути по 60°, а між собою...
НезнайкаФдпун НезнайкаФдпун  10.12.2020 13:45
Помножте вектор a=(-3;5); на 2, на 3, на -7, на 1,2 і на 1/3. 9 клас...
али5553 али5553  10.12.2020 13:46
Відрізок MB — перпендикуляр до площини рівностороннього трикутника ABC . Знайдіть кут між площинами ABM і CBM....
indyouk014 indyouk014  13.12.2021 02:04
, Задан вектор 4 (2; — 4) и точка А (-6; 2).Запишите уравнения прямой, проходящей через точку А, если: а) прямая параллельна вектору ā...
Ly3577 Ly3577  13.12.2021 02:06
Один из смежных углов в 3 раза больше чем второй. Найдите больший из этих углов....
senyazer senyazer  13.12.2021 02:12
Один из внутренних односторонних углов, образованный в результате пересечения двух параллельных прямых секущей, на 50° больше чем второй. Найдите наименьший из соответствующих...
Катя7544 Катя7544  13.12.2021 03:13
Здравствуйте, выручайте, у меня сегодня экзамен по Начертательной геометрии. Вот условия: Построить треугольник в изометрии и диметрии: 1)h35,L26,m20,k5 2h24,L20,m20,k5...

Популярные вопросы