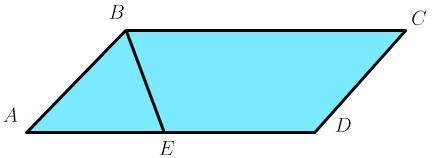
Биссектриса тупого угла параллелограмма делит противоположную сторону в отношении 3 : 6, считая от вершины острого угла. Найди большую сторону параллелограмма, если его периметр равен 24.
Другие вопросы по теме Геометрия
Популярные вопросы
- Сочинение на тему «незабываемые страницы поэмы „полтава“ „...
1 - 219. можно ли, используя только цифры 2 и 5, записать: 1) чётное...
1 - Сочинение на тему какими игрушка интересуются современные дети...
2 - Чи потрібна людині внутрішня краса? (твір)...
2 - 4.какими чертами характера влечет пугачев...
1 - Обчисліть довжину двійкового коду деякого тексту за умови що символи...
1 - Людии, мне нужно прочитать капитанскую дочку и искать краткое содержание...
2 - Почему архитектуру считают летописью человечества? !...
2 - Сравните 147000 сантиметров квадратных и 14700 дециметров квадратных...
1 - Маса 18 л меду 21 кг 60 г . яка маса 72 л...
3
Пусть АЕ равно 3х, тогда ED 6х.
Биссектриса параллелограмма отсекает от него равнобедренный треугольник.
Значит, треугольник ABE - равнобедренный.
Тогда :
АЕ=АВ= 3х.
Периметр параллелограмма можно вычислить по формуле :
Р(ABCD) = 2(АВ+AD)
24 = 2(3х+3х+6х)
24 = 12х*2
24 = 24х
х = 1.
Большая сторона AD = 3х+6х = 9х = 9*1 = 9.
ответ: 9.