. биссектриса острого угла прямоугольного треугольника АВС делит катет на отрезки равные 10см и 26 см. найдите площадь треугольника.

Ответы

lizokturina 07.09.2021 19:26

По свойству биссектрисы: CD/AD = BC/AB

10/26 = BC/AB ⇒ BC/AB = 5/13 = sin A

С другой стороны BC/AB = cos B, тогда, используя основное тригонометрическое тождество, получаем

$\sin B=\sqrt{1-\cos^2B}=\dfrac{12}{13}=\dfrac{AC}{AB}$

Но так как AC = 26 + 10 = 36 см, то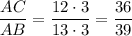 $\dfrac{AC}{AB}=\dfrac{12\cdot3}{13\cdot3}=\dfrac{36}{39}$ откуда AB = 39 см

S = 1/2 * AC * AB * sin A = 1/2 * 36 * 39 * 5/13 = 270 см²

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Геометрия

Таня13151814 31.08.2019 13:50

Onoo 31.08.2019 13:50

ISMAL2009 31.08.2019 13:50

7534558 13.08.2019 09:30

Dover1488 13.08.2019 09:30

тлрп 01.04.2021 09:27

, СОЧ Хотя бы с одним заданием, очень !...

Margarita12071 01.04.2021 09:26

mgam56 01.04.2021 09:26

Noyaneya 01.04.2021 09:26

Карина12345654321 01.04.2021 09:25

. биссектриса острого угла прямоугольного треугольника АВС делит катет на отрезки равные 10см и 26 см. найдите площадь треугольника.​