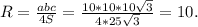Бічні сторони і менша основа рівнобічної трапеції дорівнюють 10см, один з її кутів дорівнює 60°. Знайдіть радіус кола, описаного навколо даної трапеції.
Другие вопросы по теме Геометрия
Популярные вопросы
- Чем отличаются childrens и children s? whose are these hats? -they...
2 - Расскажите о типах сказуемых в безличном предложении . примеры...
3 - Украденное время это волшебная сказка...
3 - 1. понятие, обозначающее группу — структурную единицу общества: а)...
2 - Докажите что сечение правильного прямоугольного параллелепипеда авсда1в1с1д1...
3 - Первый столбик на 20% короче другого. чтобы их подравнять, первый...
3 - Составить реакции (галогенирование,гидрогалогенирование,горение )...
2 - Как изменится сила притяжения между телами,если расстояние между...
2 - Іәріпінен басталатын немесе і әріпі көбірек мақал керек өтіні...
3 - Девочка с камнем найдите олицетворения...
2
ответ: R=10
Объяснение: Радиус окружности, описанной около трапеции, можно найти как радиус окружности, описанной около из одного из двух треугольников, на которые трапецию делит ее диагональ.
1) ∠B=120°
По теореме косинусов имеем:
AC²=AB²+BC²-2AB*BC*cos∠B
AC²=100+100+2*10*10*0.5
AC²=300
AC=10√3.
2) SΔABC=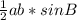 =
=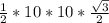 =
=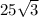
3)