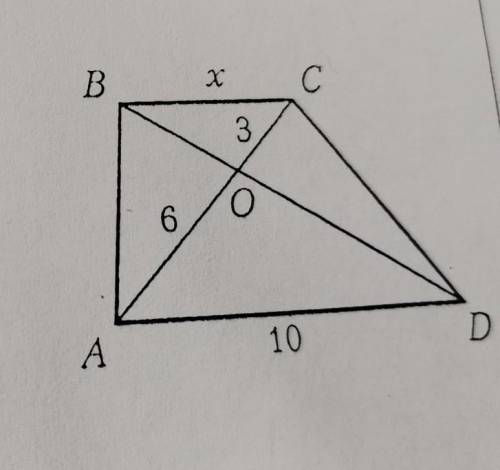
АВСD – трапеция. По данным на рисун-
ке найдите BC.​

Для решения задачи нам понадобятся свойства трапеции.

1. В первую очередь, мы знаем, что параллельные стороны трапеции равны. Это означает, что AB = CD.

2. Также, если мы нарисуем высоту трапеции из одной из вершин основания, она будет перпендикулярна этому основанию и будет делить его на две равные части. В данном случае, это будет высота из вершины C. Обозначим ее как h.

3. Зная свойства прямоугольного треугольника, мы можем использовать теорему Пифагора. В данном случае, вершиной прямоугольника является точка M, а основаниями – AB и CD. Так как AM = 10 и DM = 8, то получаем следующее уравнение:
AM^2 = CM^2 + AC^2.
10^2 = (h)^2 + (AB/2)^2.
100 = h^2 + (AB/2)^2.

4. Мы можем также заметить, что у нас имеется прямоугольный треугольник BCM, где CB – это основание равнобедренной трапеции, а BM – это половина длины основания AB. Используя теорему Пифагора, можно записать следующее уравнение:
BC^2 = h^2 + (AB/2)^2.

Теперь давайте объединим два уравнения, чтобы найти также длину BC:
100 = h^2 + (AB/2)^2,
BC^2 = h^2 + (AB/2)^2.

Теперь у нас есть система из двух уравнений с двумя неизвестными (h и AB). Мы можем решить эту систему, чтобы найти значения h и AB, а затем найти длину BC.

Для решения системы уравнений можно воспользоваться методом подстановки или методом сложения/вычитания. Решение этой системы в данном случае может быть непростым без каких-либо численных данных о длинах сторон трапеции или значения высоты.