АВСД-ромб.угол А=45 АС=8 сантиметрам найдите площадь ромба.

АВСД-ромб. Угол ∠А=45°,  АС=8 см. Найдите площадь ромба.​

Решение

∠В=180°-45°=135° по свойству односторонних углов.

Пусть сторона ромба х см, тогда по т косинусов  для ΔАВС  имеем

АС²=х²+х²-2*х*х*cos135° , cos135°=cos(90°+45°)=-cos45°=-√2/2 ,

8²=2х²+2*х²*(√2/2)

64=x²(2+√2) , x²=.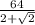

S(ромба)=ВА*ВС*sin135°=x*x*(√/2)=x²*(√2/2) = *=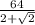

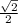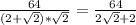
или S(ромба)=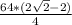 = 32(√2-1) ( см²).