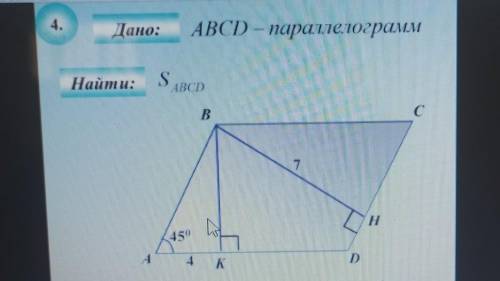
АВСD-паралелограм найти площадьABCD?BH-7 AK-4 угол А 45 градусов​

Для нахождения площади параллелограмма ABCD, мы можем воспользоваться следующей формулой:

Площадь ABCD = основание * высота.

1. Основание параллелограмма - это сторона AB, которая имеет длину 7 см.
2. Высота параллелограмма - это перпендикуляр, опущенный из вершины C на сторону AB. Чтобы найти высоту, нам необходимо знать длину стороны CK и значение угла А.

У нас уже есть длина стороны AK, которая равна 4 см. Теперь нам нужно найти сторону CK и угол А.

3. Чтобы найти сторону CK, мы можем воспользоваться теоремой Пифагора. В треугольнике AKC, где AK = 4 см и угол А = 45 градусов, две из сторон являются известными, поэтому мы можем использовать теорему Пифагора, чтобы найти третью сторону CK.

Для этого мы можем использовать следующее решение :

AK^2 + CK^2 = AC^2,
4^2 + CK^2 = AC^2,
16 + CK^2 = AC^2.

4. Чтобы найти угол АСК, мы можем использовать теорему косинусов. В треугольнике AKC, где AK = 4 см, CK - найденное значение в предыдущем шаге, и угол А = 45 градусов, мы можем использовать следующую формулу:

AC^2 = AK^2 + CK^2 - 2 * AK * CK * cos(АСК).

Мы ссылается на хорду AD в условии, чтобы этот метод использовать для того исчисления сторон основания параллелограмма ABCD.

Используя эти шаги, мы можем найти длину стороны CK и значение угла А, а затем использовать их для нахождения основания и высоты параллелограмма ABCD, и в завершение, по формуле, найдем её площадь.