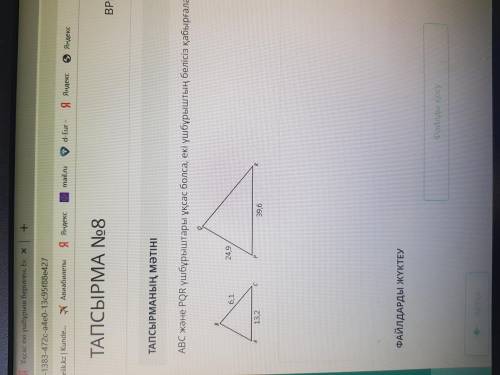
АВС жане PQR ушбурыштары уксас болса, екы ушбурыштын белысыз

Кабыргаларын табыныз.

Для решения данной задачи, нам необходимо использовать знания о параллельности и сходстве треугольников.

Начнем с того, что мы видим, что треугольник ABC и треугольник PQR параллельны, то есть соответствующие стороны треугольников параллельны (AB || PQ, BC || QR, AC || PR). Также мы знаем, что сторона AB соответствует стороне PQ, сторона BC соответствует стороне QR, а сторона AC соответствует стороне PR.

Если мы уже знаем две пары соответствующих сторон, мы можем утверждать, что треугольники подобны друг другу. В данном случае, треугольник ABC и треугольник PQR являются подобными.

Теперь давайте найдем отношение длин сторон треугольников. Для этого мы будем использовать соотношение длин сторон параллельных треугольников.

Для сторон AB и PQ:
AB/PQ = BC/QR

Подставляем известные значения:
4/6 = 5/QR

Мы можем умножить обе стороны уравнения на QR, чтобы избавиться от знаменателя:
4QR = 6*5
4QR = 30

Теперь делим обе стороны уравнения на 4, чтобы найти значение QR:
QR = 30/4 = 7.5

Таким образом, длина стороны QR равна 7.5.

Далее, мы можем найти отношение длин сторон BC и QR, так как они также являются соответствующими сторонами параллельных треугольников.

Для сторон BC и QR:
BC/QR = AC/PR

Подставляем известные значения:
5/7.5 = AC/(AC + 0.5)

Теперь домножим обе стороны уравнения на (AC + 0.5), чтобы избавиться от знаменателя:
5(AC + 0.5) = 7.5AC

Раскрываем скобки:
5AC + 2.5 = 7.5AC

Теперь вычитаем 5AC из обоих сторон уравнения:
2.5 = 2.5AC

Деля обе стороны на 2.5, найдем значение AC:
AC = 1

Таким образом, длина стороны AC равна 1.

Наконец, мы можем найти длину стороны PR, используя отношение длин сторон AC и PR.

Для сторон AC и PR:
AC/PR = AB/PQ

Подставляем известные значения:
1/PR = 4/6

Теперь домножим обе стороны уравнения на PR, чтобы избавиться от знаменателя:
1 = 4(PQ/6)

Умножаем обе стороны на 6/4:
1 * 6/4 = PQ
6/4 = PQ
3/2 = PQ

Таким образом, длина стороны PQ равна 3/2 или 1.5.

В результате, мы нашли значения сторон треугольника PQR:
PQ = 1.5
QR = 7.5
PR = еденица/1.

Надеюсь, это помогло понять тебе, как решить данную задачу! Если у тебя есть еще вопросы, обращайся!