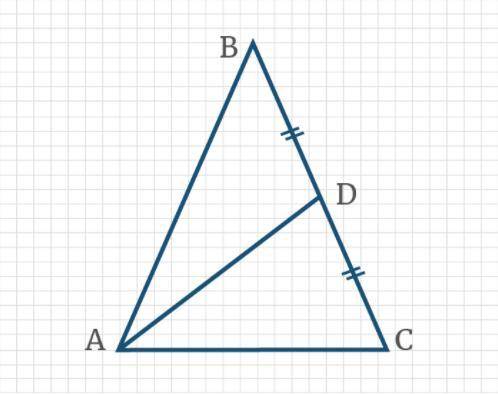
∆ АВС равнобедренный, АС = 6 см. Медиана, проведённая к боковой стороне, разбивает треугольник на два треугольника так, что периметр одного на 3 см больше периметра другого. Найти боковую сторону данного треугольника.

Для решения данной задачи, нам необходимо использовать свойства равнобедренных треугольников и знание о периметре треугольника.

Обозначим точку пересечения медианы с боковой стороной треугольника как точку М.

Известно, что АВС - равнобедренный треугольник, поэтому сторона АС равна стороне ВС. То есть, мы можем предположить, что сторона ВС также равна 6 см.

Медиана, проведенная к боковой стороне, делит треугольник на две равные части, следовательно, каждая из этих частей составляет половину от периметра и половину от сторон треугольника.

Обозначим стороны разбитого треугольника, где М делит сторону АС на две равные части, как АМ и МС.

Чтобы решить задачу, мы можем использовать следующее уравнение:

Периметр одного треугольника = Периметр другого треугольника + 3 см.

Периметр треугольника равен сумме длин его сторон.

По определению, медиана треугольника делит его пополам, поэтому МС равно половине от стороны АС, то есть МС = 6 / 2 = 3 см.

Следовательно, Периметр треугольника AMB будет равен AM + MB + AB.

Так как треугольник АВС равнобедренный, сторона AB также равна 6 см.

Известно, что периметр одного из треугольников больше периметра другого на 3 см, поэтому в данном случае Периметр треугольника AMB будет равен Периметру треугольника AMС + 3 см.

Выразим периметры треугольников через их стороны:

Периметр треугольника AMB = AM + MB + AB (Формула для нахождения периметра треугольника)

Периметр треугольника AMС = AM + MC + AC (Формула для нахождения периметра треугольника)

Теперь мы можем записать уравнение:

AM + MB + AB = AM + MC + AC + 3

Так как МС равно половине от стороны АС, то его значение равно 3 см.

Также, как мы уже обсудили ранее, сторона АС равна 6 см, а сторона АВ также равна 6 см.

Подставляем известные значения в уравнение:

AM + MB + 6 = AM + 3 + 6 + 3

Упрощаем:

AM + MB + 6 = AM + 12

Вычитаем AM из обеих частей:

MB + 6 = 12

Теперь, чтобы найти значение стороны BM, вычитаем 6 из обеих частей:

MB = 6

Таким образом, сторона BM равна 6 см.

Окончательный ответ: Длина боковой стороны треугольника равна 6 см.