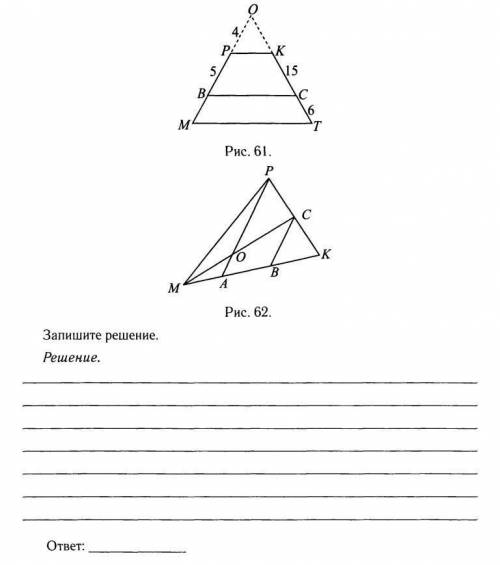
Ap || cb, mk = 36. mo = 6, pk = 30, ma : ab : bk = 2 : 3 : 7. найдите ma, oc, pc, ck. (см. рис. 62).

Давайте разберем этот вопрос пошагово:

На рисунке дан треугольник АРС и треугольник СМК. Дано, что отрезок АР параллелен отрезку СБ (или можно сказать, что линия АП параллельна линии СВ).

Также дано, что мк = 36, мо = 6 и рк = 30.

Мы должны найти значения ma, oc, pc, ck.

Известно, что ma : ab : bk = 2 : 3 : 7. Это означает, что отношение длин отрезков ma, ab и bk равно 2 : 3 : 7. Мы можем использовать это отношение, чтобы найти значение ma, поскольку это единственное значение, которое мы не знаем.

Шаг 1: Найдем значение ma.
Известно, что ma : ab : bk = 2 : 3 : 7. Мы можем записать это в виде пропорции:
ma/ab = 2/3
Теперь давайте найдем значение ab, чтобы использовать его в пропорции.
Известно, что ма + ат = 6 (в соответствии с треугольником СМК). Поскольку ма = 2/9 * рабочей нагрузки и mk = 36, мы можем записать это в виде уравнения:
2/9 * рабочая нагрузка + ат = 6 (*)
Также известно, что ма + аб + вк = 30 (в соответствии с треугольником АРС). Поскольку ма = 2/9 * рабочей нагрузки, это может быть записано как:
2/9 * рабочая нагрузка + аб + вк = 30 (**)

Чтобы найти значения ат и аб, нам понадобится решить эти два уравнения одновременно.

Шаг 2: Найти значение ат и аб.
Чтобы решить систему уравнений (\*), (**), мы можем сначала выразить ат через аб и решить уравнение только с помощью аб.

Из уравнения (\*) мы можем выразить ат:
ат = 6 - 2/9 * рабочая нагрузка
Затем, подставляя это значение ат в уравнение (**) и решая его относительно аб, получаем:
2/9 * рабочая нагрузка + аб + вк = 30
аб = 30 - вк - 2/9 * рабочая нагрузка

Теперь, подставляя это значение аб в уравнение (*), мы можем найти значение ат:
ат= 6 - 2/9 * рабочая нагрузка

Шаг 3: Найти значения ma, oc, pc, ck.
Теперь мы можем использовать найденные значения ат и аб, чтобы найти значения ma, oc, pc и ck.

- ma: мы уже знаем отношение ма и аб: ма/аб = 2/3. Подставляя найденное значение аб, мы можем найти:

ма = 2/3 * аб

- oc: мы знаем, что oc = ma + оп. Подставляя найденное значение ma и известное значение оп (6), мы можем найти:

oc = ma + 6

- pc: мы знаем, что сумма длин отрезков pc и ck равна вк (в соответствии с треугольником СМК). Мы уже нашли значение аб и знаем значение вк (30), поэтому мы можем вычислить pc следующим образом:

pc = вк - ck

- ck: как только мы найдем значение pc, мы можем использовать его, чтобы найти ck:

ck = вк - pc

Таким образом, вычислив все шаги, мы найдем значения ma, oc, pc и ck.