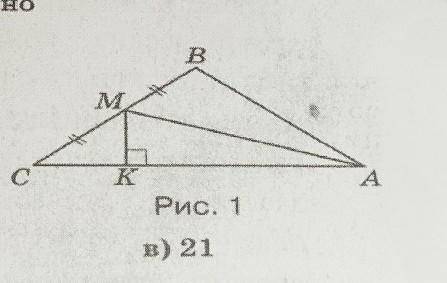
AM - медиана равнобедренного треугольника ABC (рис. 1). Точка K лежит на его основании AC так, что отрезок MK перпендикулярен AC. Найдите длину стороны AC данного треугольника, если CK = 11
Другие вопросы по теме Геометрия
Популярные вопросы
- Где и когда была впервые издана книга повесть о настоящем человеке...
3 - Напиши букву,которая обозначает первый звук в слове скворечник...
2 - На спектакле за 3 дня побывало 848 детей в1 день спетаклеь смотрели...
3 - Complete the sentences with the correct from of these verbs : * turn...
2 - Надо. 3 - 4 предложение свое мнение о каждом высказывании. 1) most...
2 - Напишите , текст на тему моя любимая музыка. максимум 5 !...
3 - Уисполнителя аккорд две команды, которым присвоены номера: 1. отними...
3 - 27+27/9*6/4*9-39/7=? 5*5+15/8*9+45-18/8=?...
2 - Скажите мне как найти тридцать сотых 7000 рублей?...
2 - Замените словосочетания, используя приставку при-. площадь у ; посёлок,расположенный...
1
Свойство медианы: медиана в треугольнике делит основание пополам и перпендикулярна ему.
Из условия задачи известно, что MK перпендикулярна AC. Также, по свойству медианы, точка M должна быть серединой стороны BC.
Рассмотрим треугольник ABC. Так как он равнобедренный, то AB = AC. Обозначим сторону треугольника AB как x.
Так как M является серединой стороны BC, то BM = MC = x/2.
Поскольку CK = 11, а BM = MC = x/2, то BK = x/2 - 11.
Рассмотрим треугольник BCK. Известно, что сумма длин двух сторон треугольника всегда больше длины третьей стороны. Поэтому:
BC + BK > CK
x + (x/2 - 11) > 11
Решаем это неравенство:
3x/2 - 11 > 11
3x/2 > 22
3x > 44
x > 44/3
Таким образом, сторона треугольника AC должна быть больше 44/3. Ответом на задачу будет x > 44/3.