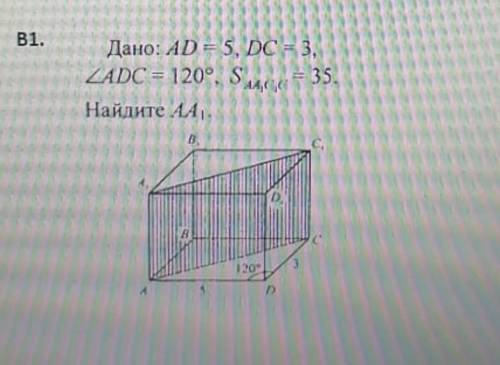
AD=5, DC=3, угол ADC =120°, Saa1c1c=35.
Найдите АА1
Другие вопросы по теме Геометрия
Популярные вопросы
- 2. Complete the questions using the verbs below....
1 - Прочитайте текст. Определите его тему и коммуникативную задачу. Определите данную...
2 - В приведённом ниже ряду найдите понятие, которое является обобщающим для всех...
1 - -- Оберіть та виконайте одне із завдань, що зацікавило вас найбільше.1. Накресліть...
2 - 3) 9,15 + (x – 8,5) = 21,77;...
3 - Христофор Колумб как он открыл южную америку...
3 - Получение кислород и изучить его свойства...
1 - 5. На карте масштаба 1: 5000 2 см соответствуют тому, сколько километров на поверхности?...
1 - Написать спартанский метод ведения битвы (спартанская стратегия...
3 - с муз. литературой! Здесь нужно посмотреть откуда взяты фрагменты. P. S. : Извините...
1
Сначала, определим значение угла CAD. Мы знаем, что угол ADC = 120°, а BC - прямая, следовательно, угол BCD = 180° - 120° = 60°.
Так как треугольник BCD - равносторонний, то угол CBD = 60°. Теперь мы можем определить угол CAD, используя факт, что сумма углов в треугольнике равна 180°:
CAD = 180° - CBD - BCD = 180° - 60° - 60° = 60°.
Теперь мы можем решить треугольник ADC. Мы знаем длины его сторон - AD = 5 и DC = 3, а также угол ADC = 120°.
Мы можем использовать теорему синусов, чтобы найти длину стороны AC. Формула теоремы синусов выглядит так:
AC / син(ADC) = DC / син(DAC).
Давайте подставим известные значения:
AC / син(120°) = 3 / син(60°).
Теперь найдем значения синусов 120° и 60°:
син(120°) = √3 / 2,
син(60°) = √3 / 2.
Подставляем эти значения:
AC / (√3 / 2) = 3 / (√3 / 2).
Упрощаем выражение, умножая каждую сторону на (√3 / 2):
AC = (3 * (√3 / 2)) / (√3 / 2).
Окончательно, упрощаем выражение с помощью сокращения и получаем значение AC:
AC = 3т.
Теперь у нас есть все стороны треугольника AAC1. Мы знаем, что сторона AA1 равна половине стороны AAC1, следовательно:
AA1 = AC / 2.
Подставляем значение AC:
AA1 = (3т) / 2.
Таким образом, ответ на задачу составляет AA1 = (3т) / 2.