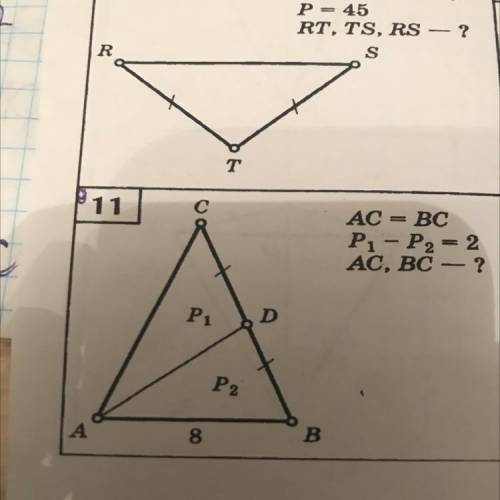
AC = BC
P1 – P2 = 2
AC, BC - ?

ответ:AC,BC=10

Объяснение:AC - AB =2

AB=8[по условию]

AC=x

X-8=2. Решаем

Х=8+2

.X=10=AC

AC=CB[по условию]. => AC,AB=10

ответ:AC.AB=10

Сори не знаю мне отвечаю потому что нужен бал для вопроса.

Добрый день! Очень рад стать вашим учителем и помочь с этим вопросом.

Чтобы найти значения AC и BC, нам нужно использовать информацию, которую мы имеем. Давайте разберемся пошагово.

1) У нас дано, что AC = BC. Это означает, что отрезки AC и BC имеют одинаковую длину.

2) Далее, у нас есть выражение P1 - P2 = 2. Здесь P1 обозначает сумму длин отрезков AC и BC, а P2 обозначает сумму длин отрезков AD и BD.

3) Рассмотрим треугольник ABC. У него есть три стороны: AB, BC и AC. Мы знаем, что AC = BC, так что можно записать P1 = AB + BC.

4) Теперь рассмотрим треугольник ABD. У него также есть три стороны: AB, AD и BD. Мы знаем, что AC = BC, а значит AB = AD + BD. Тогда можно записать P2 = AB + AD + BD.

5) Так как у нас есть выражение P1 - P2 = 2, мы можем подставить выражения из шагов 3 и 4 и записать AB + BC - AB - AD - BD = 2.

6) Заметим, что AB сокращается, и остается BC - AD - BD = 2.

7) Мы также знаем, что AD + BD = AB по свойству треугольника. Подставляем это равенство в выражение и получаем BC - AB = 2.

8) Но мы уже знаем, что AC = BC, а также AB = AD + BD, поэтому мы можем переписать это равенство как AC - AB = 2.

9) Теперь вспомним, что мы также знаем, что AC - BC = 0, так как эти отрезки имеют одинаковую длину.

10) Соединим выражения из шагов 8 и 9 и получаем AC - AB + AC - BC = 2 + 0, что приводит к 2AC - AB - BC = 2.

11) Теперь мы можем использовать информацию о том, что AC = BC, чтобы упростить это выражение. Подставляем AC вместо BC и получаем 2AC - AB - AC = 2.

12) Упрощаем выражение и получаем AC - AB = 2.

Итак, ответ на вопрос "AC, BC - ?" будет "AC - AB = 2". В этом выражении мы используем факт, что отрезки AC и BC имеют одинаковую длину, и используем информацию о сумме отрезков P1 и P2.