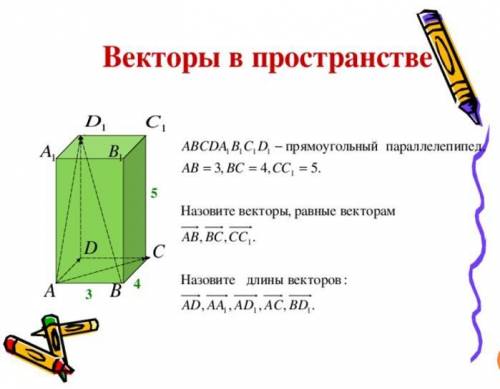
ABCDA1B1C1D1 - прямоугольный параллелепипед. AB = 3, BC = 4, CC, = 5.
Назовите векторы, равные векторам
AB, BC, CC1,
Назовите длины векторов:
AD, AA1, AD1, AC, BD1

Давайте начнем с названия векторов.

1) Вектор AB:
AB - вектор, направленный от точки A к точке B. Его направление может быть обозначено как "вправо" или "по оси x". Его длина равна расстоянию между точками A и B, в данном случае это равно 3.

2) Вектор BC:
BC - вектор, направленный от точки B к точке C. Его направление может быть обозначено как "вверх" или "по оси y". Его длина равна расстоянию между точками B и C, в данном случае это равно 4.

3) Вектор CC1:
CC1 - вектор, направленный от точки C к точке C1. Его направление также может быть обозначено как "вверх" или "по оси y". Его длина равна расстоянию между точками C и C1, в данном случае это равно 5.

Теперь перейдем к длинам векторов:

1) Длина вектора AD:
AD - вектор, направленный от точки A к точке D. Он проходит сквозь всю высоту параллелепипеда и называется диагональю. Длина данного вектора может быть найдена с помощью теоремы Пифагора:
AD = √(AB² + BC² + CC1²) = √(3² + 4² + 5²) = √(9 + 16 + 25) = √50

2) Длина вектора AA1:
AA1 - вектор, направленный от точки A к точке A1. Он также проходит сквозь всю высоту параллелепипеда. Его длина также можно найти с помощью теоремы Пифагора:
AA1 = √(AB² + BC²) = √(3² + 4²) = √(9 + 16) = √25 = 5

3) Длина вектора AD1:
AD1 - вектор, направленный от точки A до точки D1. Он находится на одной и той же высоте, что и вектор AD. Следовательно, его длина также равна √50.

4) Длина вектора AC:
AC - вектор, направленный от точки A до точки C. Он лежит в плоскости осей x и y, поэтому его длина может быть найдена с использованием теоремы Пифагора:
AC = √(AB² + BC²) = √(3² + 4²) = √(9 + 16) = √25 = 5

5) Длина вектора BD1:
BD1 - вектор, направленный от точки B до точки D1. Он находится на одной и той же ширине, что и вектор BD. Следовательно, его длина также равна 4.

Надеюсь, эти объяснения и решение помогли вам лучше понять и ответить на ваш вопрос. Если у вас остались какие-либо вопросы, пожалуйста, не стесняйтесь задавать их.