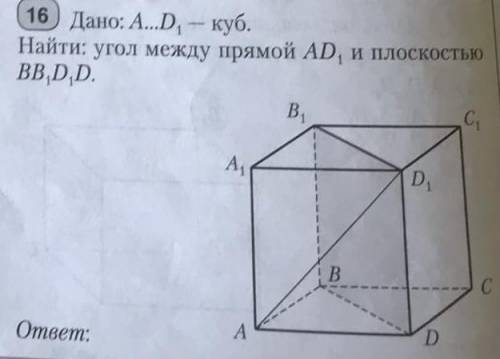
Abcda1b1c1d1 - куб. найдите угол между прямой ad1 и плоскостью bb1d1d

Чтобы найти угол между прямой ad1 и плоскостью bb1d1d, нам понадобятся знания о векторах и их свойствах.

Давайте начнем с определения векторов. Вектор - это математический объект, который имеет направление и длину. Векторы представляются в виде стрелок на графике и могут быть использованы для представления перемещений или сил.

Для начала, посмотрим на заданную нам фигуру - куб abcda1b1c1d1. Прямая ad1 проходит через вершину a и точку d1 и задается двумя векторами - ad и dd1. А плоскость bb1d1d задается третьим вектором - bb1.

Для нахождения угла между прямой и плоскостью, мы будем использовать три основные формулы:

1. Формула проекции вектора на плоскость.
2. Формула для нахождения скалярного произведения двух векторов.
3. Формула для нахождения длины вектора.

Первым шагом нам необходимо найти проекцию вектора ad на плоскость bb1d1d. Проекция вектора на плоскость - это вектор, перпендикулярный плоскости и лежащий в этой плоскости.

Чтобы найти такую проекцию, мы будем использовать формулу: прекция = ad - (ad * n) * n, где ad - заданный вектор, n - вектор, нормальный к плоскости.

Для того чтобы найти вектор n, нам нужно использовать векторное произведение двух векторов, лежащих в плоскости bb1d1d. Давайте назовем их b1b и bd1. Векторное произведение двух векторов - это вектор, перпендикулярный плоскости, который имеет направление, определяемое правилом левой руки.

Теперь, чтобы найти вектор n, мы можем использовать формулу: n = b1b x bd1, где x - операция векторного произведения.

Далее, мы находим проекцию вектора ad на плоскость bb1d1d, подставляя найденный вектор n в формулу проекции. Таким образом, мы получаем проекцию вектора ad на плоскость.

И наконец, используя формулу для нахождения скалярного произведения двух векторов: ad * proj, где ad - изначальный вектор, proj - проекция вектора ad на плоскость, мы получаем скалярное произведение этих векторов.

Чтобы найти угол между прямой ad1 и плоскостью bb1d1d, мы используем формулу: угол = arccos((ad * proj) / (||ad|| * ||proj||)), где ||ad|| и ||proj|| - длины векторов ad и proj соответственно, а arccos - обратная функция косинуса.

Вот пошаговое решение:

Шаг 1: Найдем векторы ad и dd1.
ad = a - d1 = (0,0,0) - (1,1,1) = (-1,-1,-1)
dd1 = d - d1 = (1,1,1) - (1,1,1) = (0,0,0)

Шаг 2: Найдем вектор n, нормальный к плоскости bb1d1d.
b1b = b1 - b = (1,0,1) - (0,0,0) = (1,0,1)
bd1 = b1d1 = b1 - d1 = (1,0,1) - (1,1,1) = (0,-1,0)

n = b1b x bd1 = ((0,0,0,-1)(0,1,-1)) - ((0,1,-1)(0,0,0,-1)) = (-1,-0,-1)

Шаг 3: Найдем проекцию вектора ad на плоскость bb1d1d.
proj = ad - (ad * n) * n = (-1,-1,-1) - ((-1,-1,-1)(-1,-0,-1)) * (-1,-0,-1) = (-1,-1,-1) - (1) * (-1,-0,-1) = (-1,-1,-1) + (-1,-0,-1) = (-2,-1,-2)

Шаг 4: Найдем скалярное произведение ad * proj.
ad * proj = (-1,-1,-1) * (-2,-1,-2) = -1 * -2 + -1 * -1 + -1 * -2 = 2 + 1 + 2 = 5

Шаг 5: Найдем длины векторов ad и proj.
||ad|| = sqrt((-1)^2 + (-1)^2 + (-1)^2) = sqrt(3)
||proj|| = sqrt((-2)^2 + (-1)^2 + (-2)^2) = sqrt(9) = 3

Шаг 6: Найдем угол между прямой ad1 и плоскостью bb1d1d.
угол = arccos((ad * proj) / (||ad|| * ||proj||)) = arccos(5 / (sqrt(3) * 3))

Таким образом, угол между прямой ad1 и плоскостью bb1d1d равен arccos(5 / (sqrt(3) * 3)).