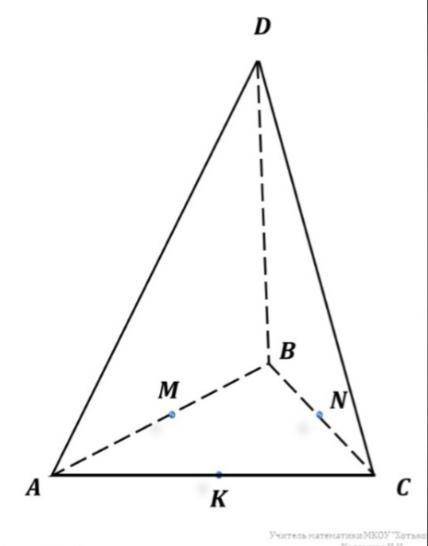
ABCD-тетраэдр. Точки M,N,K,-середины ребер AC,BC,CD.AB=6,BC=5,BD=7. Найдите длины векторов: а) АВ, ВС, BD, NM, BN, NK; б) СВ, BA, DB, NC, KN

Давайте начнем с рассмотрения длин векторов.

а) Длина вектора AB:
Для нахождения длины вектора AB нам нужно найти расстояние между точками A и B. По условию, мы знаем, что AB = 6, поэтому длина вектора AB равна 6.

Длина вектора BC:
Аналогично, для нахождения длины вектора BC нам нужно найти расстояние между точками B и C. Мы знаем, что BC = 5, поэтому длина вектора BC равна 5.

Длина вектора BD:
Для нахождения длины вектора BD нам нужно найти расстояние между точками B и D. Мы знаем, что BD = 7, поэтому длина вектора BD равна 7.

Длина вектора NM:
Чтобы найти длину вектора NM, нам нужно найти расстояние между точками N и M. Так как N и M являются серединами ребра AC, то длина вектора NM будет равна половине длины вектора AC. Мы знаем, что AB = 6, поэтому AC = 2 * AB = 2 * 6 = 12. Таким образом, длина вектора NM равна половине длины вектора AC, то есть NM = 12 / 2 = 6.

Длина вектора BN:
Аналогично, чтобы найти длину вектора BN, нам нужно найти расстояние между точками B и N. Так как N является серединой ребра AC, а точка B - одним из ее концов, то длина вектора BN будет равна половине длины вектора AB. Мы знаем, что AB = 6, поэтому BN = 6 / 2 = 3.

Длина вектора NK:
Аналогично, чтобы найти длину вектора NK, нам нужно найти расстояние между точками N и K. Так как N является серединой ребра AC, а точка K - серединой ребра CD, то длина вектора NK будет равна половине длины вектора CK. Мы знаем, что CD = BD + BC, а BD = 7 и BC = 5, поэтому CD = 7 + 5 = 12. Таким образом, CK = 12 / 2 = 6, и длина вектора NK равна 6.

б) Длина вектора SV:
Для нахождения длины вектора SV нам нужно найти расстояние между точками S и V. Зная координаты этих точек, мы можем использовать формулу расстояния между двумя точками в пространстве: √((x2 - x1)^2 + (y2 - y1)^2 + (z2 - z1)^2). Однако, в условии не даны координаты точек S и V, поэтому мы не можем точно определить длину вектора SV без этой информации.

Длина вектора BA:
Так как вектор BA является противоположным вектору AB, то длина вектора BA будет равна длине вектора AB, то есть 6.

Длина вектора DB:
Аналогично, так как вектор DB является противоположным вектору BD, то длина вектора DB будет равна длине вектора BD, то есть 7.

Длина вектора NC:
Чтобы найти длину вектора NC, нам нужно найти расстояние между точками N и C. Так как N является серединой ребра AC, а точка C - одним из ее концов, то длина вектора NC будет равна половине длины вектора AC. Мы уже рассчитали ранее, что AC = 12, поэтому NC = 12 / 2 = 6.

Длина вектора KN:
Аналогично, чтобы найти длину вектора KN, нам нужно найти расстояние между точками K и N. Так как K является серединой ребра CD, а точка N - серединой ребра AC, то длина вектора KN будет равна половине длины вектора CK. Мы уже рассчитали ранее, что CK = 6, поэтому KN = 6 / 2 = 3.

К сожалению, без дополнительной информации о координатах точек S и V, мы не можем точно определить длину вектора SV.