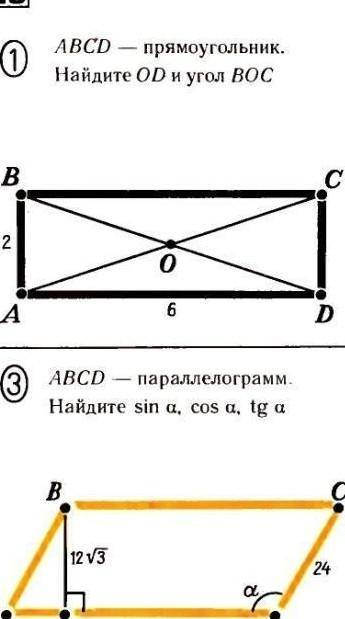
abcd прямоугольник найдите od и угол boc ab 2 ad 6
​

Для начала разберемся с обозначениями на рисунке: - Прямоугольником ABCD обозначен четырехугольник, в котором углы A и C прямые. - Точка O указывает на центр прямоугольника, то есть точку пересечения его диагоналей. - Точки D и B указывают на вершины прямоугольника, по которым мы должны найти значения. Теперь перейдем к первой части вопроса: найдем значение OD. У нас есть три данные: AB = 2 и AD = 6, а также известно, что точка O является центром прямоугольника. Мы можем заметить, что отрезок OD является половиной диагонали AC, так как точка O является ее центром. А диагональ AC является гипотенузой прямоугольного треугольника AOC, где AO и OC являются катетами. Теперь можем применить теорему Пифагора для нашего треугольника AOC: AC^2 = AO^2 + OC^2 Мы знаем, что AC = AD + DC. Подставим известные значения в это равенство: AC^2 = 6^2 + DC^2 Так как AD = 6, то DC = 6 также, так как нам дано, что AB = 2, а BC = DC. Подставим и это значение: AC^2 = 6^2 + 6^2 AC^2 = 36 + 36 AC^2 = 72 Теперь найдем значение AC, извлекая квадратный корень: AC = √72 AC = 2√18 Так как OD является половиной диагонали AC, то мы можем найти OD, разделив AC на 2: OD = (2√18)/2 OD = √18 OD = 3√2 Теперь перейдем ко второй части вопроса: найдем угол BOC. Угол BOC - это угол между отрезками BO и CO. Так как точка O является центром прямоугольника, то BO и CO являются радиусами окружности, вписанной в данный прямоугольник. Радиус окружности - это половина диагонали прямоугольника. Мы уже нашли длину диагонали AC: AC = 2√18. Теперь поделим это значение на 2, чтобы найти радиус окружности: BO = CO = AC/2 BO = CO = (2√18)/2 BO = CO = √18 BO = CO = 3√2 Изобразим на рисунке отрезки BO и CO. Теперь у нас есть два катета прямоугольного треугольника BOC, и мы можем найти угол BOC. Можно использовать треугольник BOC и тригонометрию для нахождения угла. Если мы назовем угол BOC как θ, то можем использовать тангенс: tan(θ) = BO/CO tan(θ) = (3√2)/(3√2) tan(θ) = 1 Теперь найдем угол θ, применив функцию арктангенс к обоим сторонам: θ = arctan(1) θ ≈ 45° Таким образом, OD = 3√2, а угол BOC ≈ 45°.