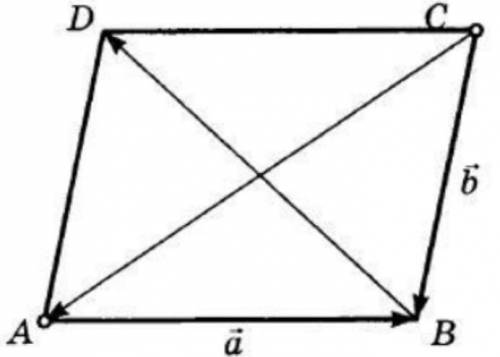
ABCD – параллелограмм. Выразите векторы бд и са через векторы а и б.

Для решения данной задачи, нам необходимо использовать свойства параллелограмма.

Изначально, мы знаем, что вектор AB является смещением от точки A к точке B. Так же, вектор BC является смещением от точки B к точке C. Таким образом, векторы AB и BC задают два стороны параллелограмма.

При этом, по свойствам параллелограмма, противоположные стороны параллелограмма равны и параллельны, следовательно вектор CD можно представить как отрицательный вектор BC. Это означает, что вектор CD будет равен -BC или CD = -BC.

Теперь мы можем выразить вектор BD через векторы AB и CD. Вектор BD можно представить как сумму векторов BC и CD, то есть BD = BC + CD. Подставляя значения, получаем BD = BC + (-BC), что равно BD = 0. Таким образом, вектор BD равен нулевому вектору, что означает, что точка B совпадает с точкой D.

Теперь осталось выразить вектор CA через векторы AB и BC. Вектор CA можно представить как сумму векторов CD и DA, то есть CA = CD + DA. Для удобства, заметим, что вектор DA можно представить как сумму векторов DB и BA, то есть DA = DB + BA.

Подставляем значения и получаем CA = CD + DA = -BC + (DB + BA). Кроме того, по свойству параллелограмма, противоположные стороны равны и параллельны, а значит вектор DB равен -BA. Подставляем это в выражение и получаем CA = -BC + (-BA + BA).

Замечаем, что вектор BA является смещением от точки B к точке A, а значит он равен вектору -AB. Подставляем это в выражение и получаем CA = -BC + (-AB + AB). Так как -AB + AB = 0, то получаем CA = -BC.

Таким образом, мы получили, что вектор BD равен нулевому вектору, а вектор CA равен -BC.