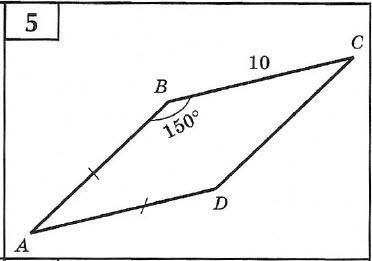
ABCD параллелограмм. Найти его площадь РЕШЕНИЕ

Т.к. АВСD параллелограмм, то АD = BC = 10.

Проведём высоту BH.

Тр. АВН - прямоугольный. Угол ВАН = 30° (т.к. сумма двух углов параллелограмма равна 180°, отсюда 180 - 150 = 30° = углу А).

В тр.АВН катет лежащий против угла в 30° равен половине гипотенузы ВН = 1/2AB. АВ = АD = 10, значит ВН = 5.

Площадь ABCD = 10 × 5 = 50

Объяснение:

Чё за рофлы, чел?

У тя куча заданий по математике решено и ты - светило науки.

S=50 квадратных единиц.

Объяснение:

Дано: ABCD параллелограмм, АВ=AD, ВС=10, ∠АВС=150°.

Найти: S - площадь ABCD.

Решение: по формуле нахождения площади параллелограмма

S=AB*BC*sin∠В

Подставим в вышеуказанную формулу известные значения:

S=AB*BC*sin150°

S=AB*10*0,5

S=AB*5

По определению параллелограмма BC=AD. То есть AD=10 единиц. Так как по условию АВ=AD, то АВ=10 единицам. Подставим в последнюю формулу полученное значение

S=10*5

S=50 квадратных единиц.