Abcd-квадрат со стороной, равной 4 см. треугольник амв имеет общую сторону ав с квадратом, ам=вм= 3см. плоскости треугольника и квадрата взаимно перпендикулярны. найдите угол между мс и плоскостью квадрата

Ответы

Anopsis 24.05.2020 02:51

Пусть MH - высота в треугольнике AMB, тогда угол MCH - искомый.

Т.к. AMB равнобедренный, то H середина AMB, т.е. AH=2

Из прямоугольного треугольника AMH имеем

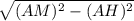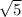
MH = $\sqrt{(AM)^{2} - (AH)^{2} }$ = $\sqrt{5}$

Из прямоугольного треугольника BCH имеем

CH =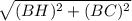 $\sqrt{(BH)^{2} + (BC)^{2} }$ = $\sqrt{20}$

тогда угол MCH можно определить по его тангенсу

tg(MCH) =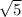 $\sqrt{5}$ / $\sqrt{20}$ = 0.5

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Геометрия

stig228 31.03.2021 19:52

Alinka291002 31.03.2021 19:54

79954236 02.11.2020 14:37

khaub456 02.11.2020 14:37

siylvio 02.11.2020 14:37

dĵdjdkdkdkdkdk 02.11.2020 14:36

выбрать правильные ответы...

Ничегосебеденёк 16.08.2019 23:20

учусь5 16.08.2019 23:20

0Karamelka0 16.08.2019 23:20

PomogitePPLez 16.08.2019 23:20

Существует ли треугольник a=3см b=2см c=2см. решение...