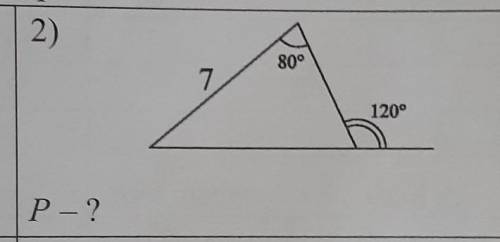
ABC треугол. AB=7 B=70° BCD=120° Найти периметр ABC​

Для того чтобы найти периметр треугольника ABC, нам нужно знать длины его сторон. В данной задаче нам дано только одно значение длины стороны AB, которая равна 7 единицам.

Чтобы найти длины остальных сторон треугольника ABC, нам понадобится использовать тригонометрические соотношения. Сначала найдем длину стороны BC.

Из условия задачи мы знаем угол B, который равен 70 градусам. Также нам дан угол BCD, который равен 120 градусам. Обратите внимание, что это внешний угол треугольника ABC.

Теорема синусов гласит, что отношение длины стороны треугольника к синусу противолежащего ей угла равно постоянной величине. Используя эту теорему, мы можем найти длину стороны BC.

Синус угла B можно вычислить по формуле: sin(B) = противолежащая сторона / гипотенуза.

Так как сторона AB является гипотенузой прямоугольного треугольника ABP (где P - точка пересечения высоты с основанием), а сторона BP является противолежащей стороной угла B, мы можем записать:
sin(B) = BP / AB.

Заменив значения в формуле, получим:
sin(70°) = BP / 7.

Теперь мы можем выразить длину стороны BP:
BP = 7 * sin(70°).

Подставив значения, получим:
BP = 7 * 0.9397 (приближенно) ≈ 6.578.

Таким образом, длина стороны BC равна приблизительно 6.578 единиц.

Теперь мы знаем длины сторон AB и BC. Чтобы найти длину стороны AC, мы можем использовать теорему косинусов. Теорема косинусов гласит, что квадрат длины противолежащей стороны треугольника равен сумме квадратов длин двух других сторон минус удвоенное произведение этих сторон на косинус внутреннего угла между ними.

Применяя эту формулу к треугольнику ABC, мы можем записать следующее уравнение:
AC^2 = AB^2 + BC^2 - 2 * AB * BC * cos(B).

Мы знаем значения AB, BC и B. Подставляя эти значения в уравнение, получаем:
AC^2 = 7^2 + 6.578^2 - 2 * 7 * 6.578 * cos(70°).

Высчитав это уравнение, получим:
AC^2 ≈ 49 + 43.23 - 91.8288 ≈ 0.4012.

Возведя обе части уравнения в квадрат, получим:
AC ≈ √0.4012 ≈ 0.633 (приближенно).

Таким образом, длина стороны AC равна приблизительно 0.633 единицы.

Теперь, когда у нас есть длины всех трех сторон треугольника ABC, мы можем найти его периметр. Периметр равен сумме длин всех сторон треугольника.

Подставляя значения, получаем:
Периметр ABC = AB + BC + AC.
Периметр ABC ≈ 7 + 6.578 + 0.633 ≈ 14.211.

Таким образом, периметр треугольника ABC равен приблизительно 14.211 единицам.